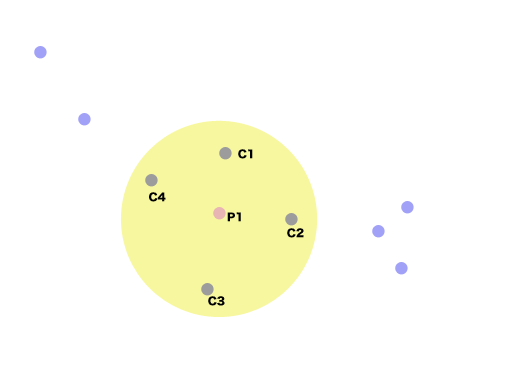
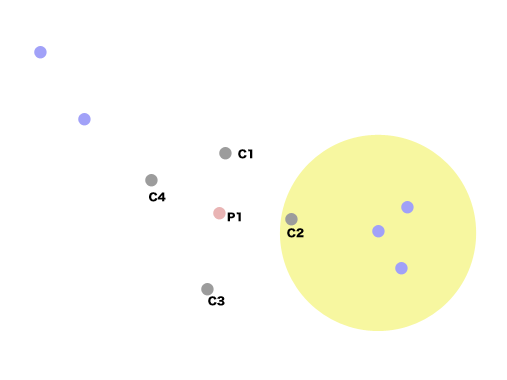
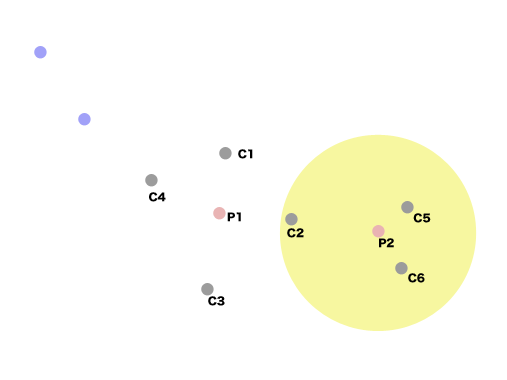
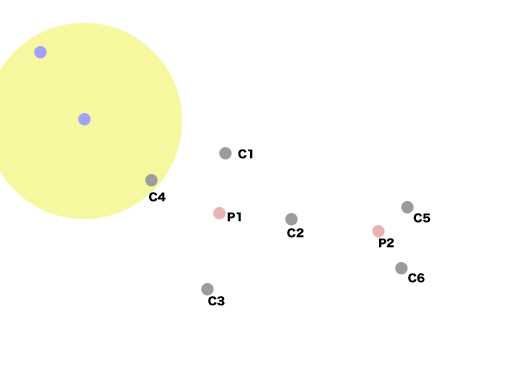
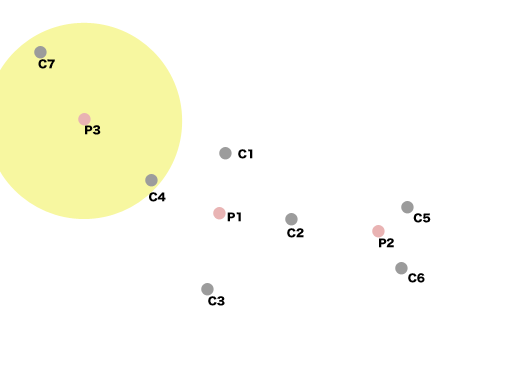
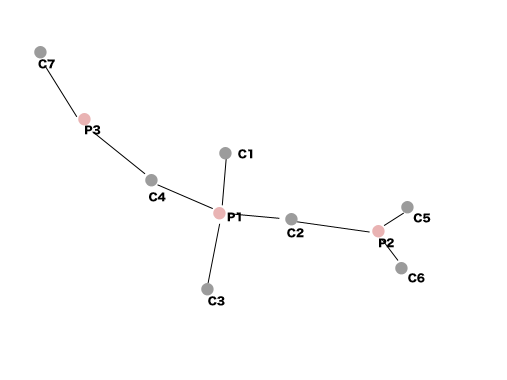
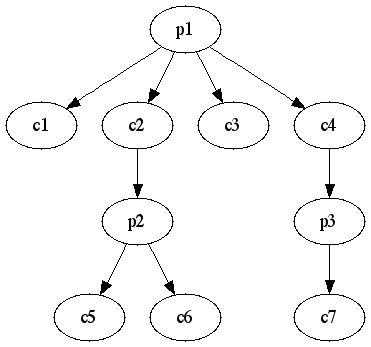
論文読んでたら、コンベンショナルなMMPの求め方が載ってたので、似たようなやり方を考えてみた。
要するに網羅的に結合を切断していって
{Scaffold; [fragment, fragment, fragment]}
っていうハッシュを作っていく。fragmentは共通のScaffoldを持つので配列中の任意のフラグメントのペアがMMPということになる。
僕の切断ルール
僕の切断ルール
- シングルボンド
- 環の一部ではない
- ボンドのどちらかの端がCであること
CHEMBL327743の結果
('CC[C@@H]([C@H](NC(=O)[C@@H]1CCCCN1CC(=O)*)/C=C/c1ccccc1)C', 'COc1cccc(c1*)OC', 'CHEMBL327743')
('CC[C@@H]([C@H](NC(=O)[C@@H]1CCCCN1C*)/C=C/c1ccccc1)C', 'COc1cccc(c1C(=O)*)OC', 'CHEMBL327743')
('CC[C@@H]([C@@H](/C=C/c1ccccc1)N*)C', 'COc1cccc(c1C(=O)CN1CCCC[C@H]1C(=O)*)OC', 'CHEMBL327743')
('CC[C@@H]([C@H](NC(=O)*)/C=C/c1ccccc1)C', 'COc1cccc(c1C(=O)CN1CCCCC1*)OC', 'CHEMBL327743')
('CC[C@@H](C(NC(=O)[C@@H]1CCCCN1CC(=O)c1c(OC)cccc1OC)*)C', '*/C=C/c1ccccc1', 'CHEMBL327743')
('COc1cccc(c1C(=O)CN1CCCC[C@H]1C(=O)N[C@H](/C=C/c1ccccc1)*)OC', 'CC[C@H](C)*', 'CHEMBL327743')
('*c1ccccc1', '*/C=C\\[C@H]([C@H](CC)C)NC(=O)[C@@H]1CCCCN1CC(=O)c1c(OC)cccc1OC', 'CHEMBL327743')
('*OC', 'CC[C@@H]([C@H](NC(=O)[C@@H]1CCCCN1CC(=O)c1c(*)cccc1OC)/C=C/c1ccccc1)C', 'CHEMBL327743')
('*OC', 'CC[C@@H]([C@H](NC(=O)[C@@H]1CCCCN1CC(=O)c1c(*)cccc1OC)/C=C/c1ccccc1)C', 'CHEMBL327743')
('*CC', 'COc1cccc(c1C(=O)CN1CCCC[C@H]1C(=O)N[C@@H](C(C)*)/C=C/c1ccccc1)OC', 'CHEMBL327743')
('CC[C@@H]([C@H](NC(=O)[C@@H]1CCCCN1CC(=O)c1c(OC)cccc1OC)/C=C/c1ccccc1)*', 'C*', 'CHEMBL327743')
('*C[C@@H]([C@H](NC(=O)[C@@H]1CCCCN1CC(=O)c1c(OC)cccc1OC)/C=C/c1ccccc1)C', 'C*', 'CHEMBL327743')
コード
どこで切断されたかどうかを明確にするために切断されたボンドにダミーアトム(atomicnumが0のアトム)をおいた。
canonicalSMILESで出力して.の文字でsplitした文字列をそのままキーに使っているが、openbabelのcanonicalizationアルゴリズムはMorgan Algorithmを改変したものを使っているのでおそらく大丈夫。
下のコードでは標準出力に書きだしたが、実際はデータベース化することになる。多分Mongo使う。
smi_string,id = clone.write(format="can")[:-1].split('\t')
frag1, frag2 = smi_string.split('.')
dbh.mmp.update({"core": frag1}, {"$push": {"frags": (frag2, id)}}, True)
dbh.mmp.update({"core": frag2}, {"$push": {"frags": (frag1, id)}}, True)
こんな感じだろうか。
以下MMPを求めるのに使ったコード
import pybel
import openbabel
import sys
input = sys.argv[1]
def mkclone(mol):
obc = openbabel.OBConversion()
obc.SetInAndOutFormats("mol", "mol")
molstring = obc.WriteString(mol)
new_mol = openbabel.OBMol()
obc.ReadString(new_mol, molstring)
return new_mol
def ring_member(rings, atom):
for i, ring in enumerate(rings):
if ring.IsMember(atom):
return i
return -1
def is_same_ring_member(rings, a1, a2):
a1_idx = ring_member(rings, a1)
a2_idx = ring_member(rings, a2)
if a1_idx == -1 or a2_idx == -1:
return False
return a1_idx == a2_idx
def detect_del_bonds(mol):
rings = mol.OBMol.GetSSSR()
del_bonds = []
for a in mol:
if a.atomicnum == 6:
for na in mol:
n_a = na.OBAtom
b = a.OBAtom.GetBond(n_a)
if b != None and b.GetBondOrder() == 1 and not is_same_ring_member(rings, a.OBAtom, n_a):
if a.OBAtom.GetIndex() < n_a.GetIndex():
del_bonds.append((a.OBAtom.GetIndex(), n_a.GetIndex()))
return del_bonds
for mol in pybel.readfile("sdf", input):
chembl_id = mol.data["CHEMBL ID"]
print chembl_id
del_bonds = detect_del_bonds(mol)
for a1, a2 in del_bonds:
clone = pybel.Molecule(mkclone(mol.OBMol))
# !!! index starts 0 but GetAtom starts 1 !!!
ob_a1 = clone.OBMol.GetAtom(a1 + 1)
ob_a2 = clone.OBMol.GetAtom(a2 + 1)
bond = ob_a1.GetBond(ob_a2)
clone.OBMol.DeleteBond(bond)
new_atom1 = clone.OBMol.NewAtom()
new_atom1.SetAtomicNum(0)
new_bond1 = clone.OBMol.NewBond()
new_bond1.SetBegin(ob_a1)
new_bond1.SetEnd(new_atom1)
new_bond1.SetBondOrder(1)
new_atom2 = clone.OBMol.NewAtom()
new_atom2.SetAtomicNum(0)
new_bond2 = clone.OBMol.NewBond()
new_bond2.SetBegin(ob_a2)
new_bond2.SetEnd(new_atom2)
new_bond2.SetBondOrder(1)
smi_string, id = clone.write(format="can")[:-1].split('\t')
frag1, frag2 = smi_string.split('.')
#print (frag1, chembl_id)
#print (frag2, chembl_id)
print (frag1, frag2, chembl_id)
Design and Use of Relational Databases in Chemistry
初めてのPython 第3版
すぐできる 量子化学計算ビギナーズマニュアル (KS化学専門書)