2011/11/17 09:05:10
ネットワーク分析は楽しいですね。普段は化合物のネットワークとかいじっているんだけど、もう少し見識を広めるために違ったタイプのネットワークの分析手法を勉強してみたくなって本書を読んでみた。
社会ネットワークとは、アクターと呼ばれる行為者としての社会単位が、その意図的・非意図的な相互行為のなかで取り結ぶ社会諸関係の集合である
これらをミクロな視点からみていくか、マクロな視点からみていくかだけど、マクロな視点だと個人の特性が失われてしまうので、これはダメらしい。自分の経験では、（ケミストリーを知らない）ケモインフォマティクスのヒトが、個々の化合物をパラメーターで潰してしまって実態とかけ離れたマクロな解釈しかできないのをよく見るので、まぁそうかなとも思う。
で、よりよい社会像を得るためにどうしたら良いのかということで、社会構造の二重性モデルを使うのが、現代の社会ネットワーク分析らしいです。
個人的に興味が湧いたのは9章の「弱い紐帯」が重要か、ブリッジが重要かという話題とネットワークは凝集的で閉鎖的がいいのか、離散的で開放的がいいのか？という話題。第三部の「ソーシャル・キャピタル研究：組織論への展開」は読み物として面白かった。
セイヤーによれば「関係」は形式的なものと実質的なものに分けられる
形式的の関係とは「ともに30歳」みたいなもので、実質的な関係の例は「夫婦」
ハイパーグラフは個人がグループに所属するような所属関係のネットワークを表すのに利用されたり、重複メンバー関係をモデル化するのに便利
これは以前教えてもらったときに調べた。
かなり教科書っぽいので、手を動かしたい場合は「ネットワーク分析 (Rで学ぶデータサイエンス 8) 」のほうが良いかも
2010/10/09 10:14:57
以前、おもむろに思いついたLeadOptimizationのシミュレーターで、networkxはgml出力できてCytoscapeでimportすればいいじゃんということに気づいてヤル気が出た。
ついでにコードもちょっと直して、活性はpIC50とかそういうレンジにしてみて、μMオーダーから上げていくようにした。
エッジは世代を表していて、黄色から緑にむけてすすんでいく。ノードの色は活性を表していて黒から赤になるにしたがって活性が向上する。最初の方は活性が振れるけど段々向上していって安定するようにしてみた。
リードホッピングとは選択されなかったより良い未来を選択しなおすことであるとするならばそのような希望はLO初期のあたりに存在すると思うのだ。
以下、書いたコード
from random import random
import networkx as nx
class Branch(object):
"""LeadOptimization flow
potency: pIC50 or such
weight : range for activity
"""
count = -1
@classmethod
def inc_count(cls):
cls.count = cls.count + 1
return cls.count
@classmethod
def get_count(cls): return cls.count
def __init__(self,potency,weight):
self.id = Branch.inc_count()
self.potency = potency
self.weight = weight
self.activity = self.potency + self.weight * random()
def make_child(self,num_childs,potency,weight):
return [Branch(self.potency + self.weight * (random()-0.5)*2,self.weight * 0.5) for i in range(num_childs)]
if __name__ == "__main__":
max_comps = 500 # total compounds
initial_branches = 1 # number of lead compounds
lead_potency = 5 # lead activity
generation = 0
G=nx.Graph()
heads = [Branch(lead_potency,2) for i in range(initial_branches)]
map(lambda b: G.add_node(b.id, activity=b.activity),heads)
while Branch.get_count() < max_comps:
new_heads = []
generation += 1
for branch in heads[:int(2+5*random())]:
for new_comp in branch.make_child(int(40*random()),branch.potency,branch.weight):
G.add_node(new_comp.id, activity=new_comp.activity)
G.add_edge(branch.id, new_comp.id, genneration=generation)
if new_comp.activity > 7:
new_heads.append(new_comp)
heads = new_heads
heads.sort(key=lambda x:x.activity)
heads.reverse()
nx.write_gml(G,"test.gml")
2010/08/18 18:44:45
MCSを求めるには比較したい二つの化合物のModular Productを求めて、それの最大クリーク探索をすればいい。
Modular Productとは
- 二つのグラフの属性の対応が同じノードが両方共隣接していてエッジの属性が同じ場合
- 二つのグラフの属性の対応が同じノードが両方共隣接していない場合
にエッジを張ったグラフ。
これを作ってあとはigraphの最大クリーク探索メソッドで
import openbabel as ob
from igraph import *
sm1 = 'OCC(N)=O'
sm2 = 'O=CC(N)=O'
obc = ob.OBConversion()
obc.SetInAndOutFormats('smi','smi')
source = ob.OBMol()
obc.ReadString(source,sm1)
source_atoms = [a for a in ob.OBMolAtomIter(source)]
target = ob.OBMol()
obc.ReadString(target,sm2)
target_atoms = [a for a in ob.OBMolAtomIter(target)]
pairs = []
for i in range(len(source_atoms)):
for j in range(len(target_atoms)):
if source_atoms[i].GetAtomicNum() == target_atoms[j].GetAtomicNum():
pairs.append((source_atoms[i].GetIdx(),target_atoms[j].GetIdx()))
p = []
for x in range(len(pairs)-1):
for y in range(x+1,len(pairs)):
u = pairs[x]
v = pairs[y]
if u[0] != v[0] and u[1] != v[1]:
sb = source.GetBond(u[0],v[0])
tb = target.GetBond(u[1],v[1])
if sb != None: sbo = sb.GetBondOrder()
if tb != None: tbo = tb.GetBondOrder()
if (sb == None and tb == None) or (sb != None and tb != None and sbo == tbo):
p.append((pairs.index(u),pairs.index(v)))
g = Graph(p)
mc = g.largest_cliques()
for c in mc:
print [pairs[i] for i in c]
実際にはline graph(エッジとノードを入れ替えたグラフ)のModular Productをもとめてクリーク探索したほうが計算量がかなり減るらしい。
が、今回はやっていない。
2010/03/10 21:56:46
ふと、つぶやいた。
例えば
- プロジェクトで500検体合成
- ひとつの親あたり5-25化合物くらいの子を合成する
- プロジェクトの人員の制限により、一度に10ラインまでしか同時に走らない
- 11番目以降はそれ以降のオプティマイゼーションは行われない
その時知りたいことは、
- {計画、合成、アッセイ、解析}というサイクルは何回まわるのか、
- 有望そうな化合物だけど、人的リソースの関係で選択されなかった歴史はどこにあるか？
- バックアップ候補の化合物はどこら辺で現れるか（初期？中期？）
あたり。
現実の系に近づけるために、親化合物にはポテンシャルがあって、近傍探索すると、ポテンシャルの近くで活性が変化するモデル。あと同じライン（ブランチ）を継続して合成すると、ポテンシャル曲線が底に近づくのと、合成もSARに関する知識がついてくるので、活性は上がりやすくなって、かつ変動幅も小さくなるようにweightはだんだん小さくなるようにしてみた。
#!/usr/bin/env python
# -*- encoding:utf-8 -*-
# kzfm <kerolinq@gmail.com>
from random import random
import networkx as nx
import matplotlib.pyplot as plt
class Branch(object):
"""LeadOptimization flow"""
count = 0
@classmethod
def inc_count(cls):
cls.count = cls.count + 1
return cls.count
@classmethod
def get_count(cls): return cls.count
def __cmp__(self, other):
return cmp(self.act, other.act)
def __init__(self,potency,weight):
self.num = Branch.inc_count()
self.potency = potency
self.weight = weight
self.act = self.potency + self.weight * random()
def make_child(self,num_childs,potency,weight):
return [Branch(self.potency + self.weight * random(),self.weight * 0.7) for i in range(num_childs)]
if __name__ == "__main__":
max_comps = 500
initial_branches = 3
nodesize = []
nrange = []
erange = []
generation = 1
heads = [Branch(0.3,1) for i in range(initial_branches)]
G=nx.Graph()
for h in heads:
nodesize.append(h.act * 30)
nrange.append(generation)
while Branch.get_count() < max_comps:
new_heads = []
generation += 1
for branch in heads[:10]:
for new_comp in branch.make_child(int(5+20*random()),branch.potency,branch.weight):
nodesize.append(new_comp.act * 30)
nrange.append(generation)
erange.append(generation)
G.add_edge(branch.num,new_comp.num)
if new_comp.act > 0.75:
new_heads.append(new_comp)
heads = new_heads
heads.sort()
nx.draw_spring(G, node_size=nodesize, node_color=nrange, edge_color=erange,alpha=0.7, \
cmap=plt.cm.hot, edge_cmap=plt.cm.hot, with_labels=False)
plt.savefig("proj.png")
んーなんかいまいち。一応活性の強弱にあわせてノードのサイズが変わるようにしてみたんだけど、大きさがわからん。
2010/01/12 10:34:45
ヒューリスティクスは割と好きだ。スパッととけないものをなんとか現実と折り合いを付けながらよりよい解を見つけるみたいな、なんとも煮え切らない美しさのなさがたまらん。インフォマティクスも似たような香りはする。
特に、「シミュレーションできない学問は学問として未成熟である」という言葉に従うのであれば、創薬研究は（学際領域）と言われている割には未成熟な学問の組み合わせのために発見的な手法の割合が増えすぎるし、精度の高い予測法の誕生もまだまだ先であろう。というわけで、発見的な探索手法は当分有用だし、学際領域故に融合部分での応用が期待されるため、アルゴリズムとしてきちんと押さえておくと色々役に立つ。
メタヒューリスティクスの数理の4章はpythonのコードが載っているので、勉強になる。
- 第4章 応用
- 4.1 グラフ分割問題
- 4.2 最大安定集合問題
- 4.3 グラフ彩色問題
- 4.4 巡回セールスマン問題
- 4.5 2次割当問題
- 4.6 多制約ナップサック問題
- 4.7 数分割問題
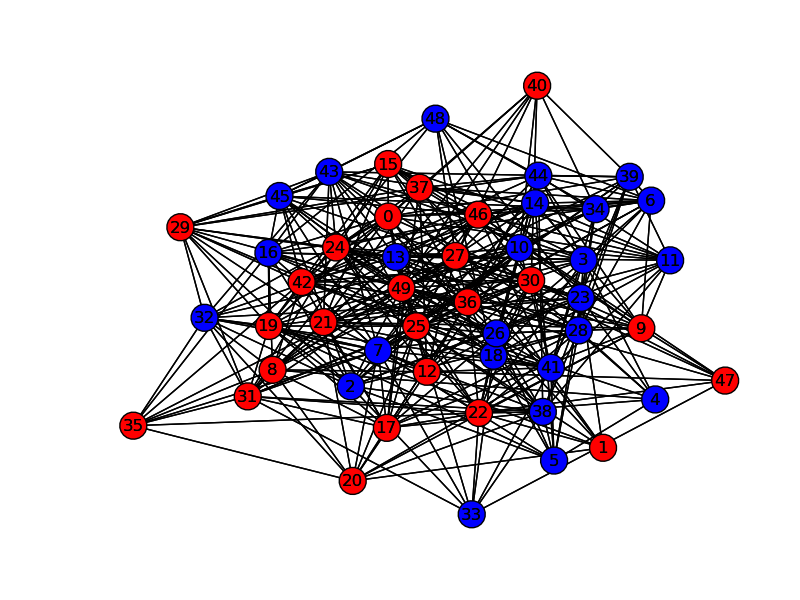
4.1のグラフ分割問題をnetworkxで可視化するように書き換えた。
import math,random
from sys import maxint as Infinity
def rnd_graph_fast(nnodes, prob):
nodes = range(nnodes)
adj = [[] for i in nodes]
i=1;j=1
logp = math.log(1.0 - prob)
while i<nnodes:
logr = math.log(1.0 - random.random())
j += 1+int(logr/logp)
while j>=i and i<nnodes:
j -= i
i += 1
if i<nnodes:
adj[i].append(j)
adj[j].append(i)
return nodes, adj
def construct(nodes):
sol = [0 for i in nodes]
for i in range(len(nodes)/2):
sol[i] = 1
return sol
def evaluate(nodes, adj, sol):
cost = 0
s = [0 for i in nodes]
d = [0 for i in nodes]
for i in nodes:
for j in adj[i]:
if sol[i] == sol[j]:
s[i] += 1
else:
d[i] += 1
for i in nodes:
cost += d[i]
return cost/2, s, d\
def find_move(part, nodes, adj, sol, s, d, tabu, tabulen, iteration):
mindelta = Infinity
istar = None
for i in nodes:
if sol[i] != part:
if tabu[i] <= iteration:
delta = s[i] - d[i]
if delta < mindelta:
mindelta = delta
istar = i
if istar != None:
return istar, mindelta
tabu = [0 for i in nodes]
return find_move(part, nodes , adj, sol, s, d, tabu, tabulen, iteration)
def move(part, nodes, adj, sol, s, d, tabu, tabulen, iteration):
i, delta = find_move(part, nodes, adj, sol, s, d, tabu, tabulen, iteration)
sol[i] = part
tabu[i] = iteration + tabulen
s[i], d[i] = d[i], s[i]
for j in adj[i]:
if sol[j] != part:
s[j] -= 1
d[j] += 1
else:
s[j] += 1
d[j] -= 1
return delta
def tabu_search(nodes, adj, sol, max_iter, tabulen):
cost, s, d = evaluate(nodes, adj, sol)
tabu = [0 for i in nodes]
bestcost = Infinity
for it in range(max_iter):
cost += move(1, nodes, adj, sol, s, d, tabu, tabulen, it)
cost += move(0, nodes, adj, sol, s, d, tabu, tabulen, it)
if cost < bestcost:
bestcost = cost
bestsol = list(sol)
return bestsol, bestcost
if __name__ == "__main__":
import networkx as nx
import matplotlib.pyplot as plt
num_nodes = 50
nodes, adj = rnd_graph_fast(num_nodes,0.3)
G=nx.Graph()
for i in range(num_nodes):
G.add_node(i)
for i in range(num_nodes-1):
for j in adj[i]:
if i < j:
G.add_edge(i,j)
pos=nx.spring_layout(G)
max_iter = 1000
tabulen = 10
sol = construct(nodes)
sol, cost = tabu_search(nodes, adj, sol, max_iter, tabulen)
rnodelist = []
bnodelist = []
for i in range(len(sol)):
if sol[i] == 1:
rnodelist.append(i)
else:
bnodelist.append(i)
nx.draw(G,pos,nodelist=rnodelist,node_color='r')
nx.draw(G,pos,nodelist=bnodelist,node_color='b')
plt.savefig("path.png")
これをちょっと変えてSimulated Annealingにできる。
2009/05/23 11:50:48
コンパートメントモデルを書くのにいちいちInkspaceを立ち上げるのもめんどうなのでGraphvizにでも頼るかと思ったらmacbookには入ってなかった。networkxもついでに入れといた。
sudo port install graphviz
sudo easy_install-2.6 pygraphviz
sudo easy_install-2.6 networkx
使う
>>> import pygraphviz as pgv
>>> d={'1': {'2': None}, '2': {'1': None, '3': None}, '3': {'2': None}}
>>> A=pgv.AGraph(d)
>>> A.layout(prog='dot')
>>> A.draw('pyg.png')
2008/11/27 21:32:14
今、僕の中でグラフブームが来てます。というわけで、バラバシ。
- 外の世界とコミュニケーションする能力は、弱い絆に支配されている
- 親しい友人は職を得るにはあまり役立たない場合が多い
- ネットワークの中で真に中心的な位置につけているのは、多数の大きなクラスターに参加しているノードだ
- ハブはいかに出現するのか？そこにはハブはいくつ存在するのか？
- 自然は普通ベキ法則を嫌うものである
- 成長しないという仮説は、現実のネットワークにはあてはまらない
- なぜスケールフリーモデルにはハブとベキ法則があらわれるのか？
- スケールフリートポロジーが意味しているのは、ネットワーク形成の各段階で何らかの組織原理が働いている
- スケールフリーモデルで新参者がどうやって成功するか？
- ウェブや社会ネットワークと量子力学の関係性
- スケールフリーネットワークのがエラー耐性を持つのはトポロジー本来の性質
2008/11/03 20:52:23
特にsubgraphの探索とか勉強したいところなんだけど、軽く脱線気味に。グラフとかネットワークは勉強してて楽しいですのう。
複雑ネットワーク入門
今野 紀雄,井手 勇介
講談社 / ￥ 2,520 ()
通常24時間以内に発送
半分くらいはグラフの基本的なことで、ゴルトン・ワトソン木、スモールワールド、スケールフリー、しきい値モデルをさらっと。
- 序章でラムゼー数
- クラスター係数
- 二部グラフ
- グラフの頂点集合が互いに素な二つの集合に分かれていること
- ケーリーの定理
- ランダムグラフのクラスター係数の期待値は本質的にはp
- ゴルトン・ワトソン過程はマルコフ連鎖
- スモールワールド性
- NWモデル
- 拡張されたサイクルと、ランダムグラフを重ね合わせたグラフ
- しきい値モデル
本書には具体的な例はほとんどないので自分で探せということか。
2008/11/01 21:39:58
GASTONが分からなくてお悩み中。参考文献とかから読まないとやっぱダメな感じ。
TODO:ここから追いかける
そのながれで、最短経路の本も読んでおく
最短経路の本
R. ブランデンベルク,P. グリッツマン
シュプリンガー・ジャパン株式会社 / ￥ 3,675 ()
通常24時間以内に発送
当分日本酒も無しだなぁ、ということで、昨日吞みきった高砂で当分は家吞み断ちだ。
中国茶用の茶器出したら、U隊長に「珍しいねー(なんかあったの？)」なんて言われてしまった。
社会ネットワーク分析の基礎―社会的関係資本論にむけて
ネットワーク分析 (Rで学ぶデータサイエンス 8)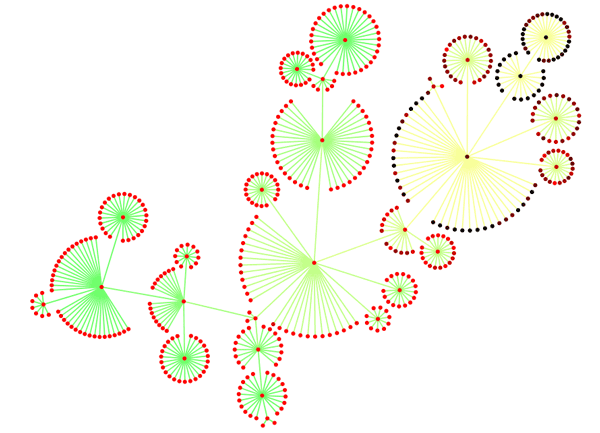
Handbook of Chemoinformatics Algorithms (Chapman & Hall/Crc Mathematical and Computational Biology)
Chemoinformatics and Computational Chemical Biology (Methods in Molecular Biology)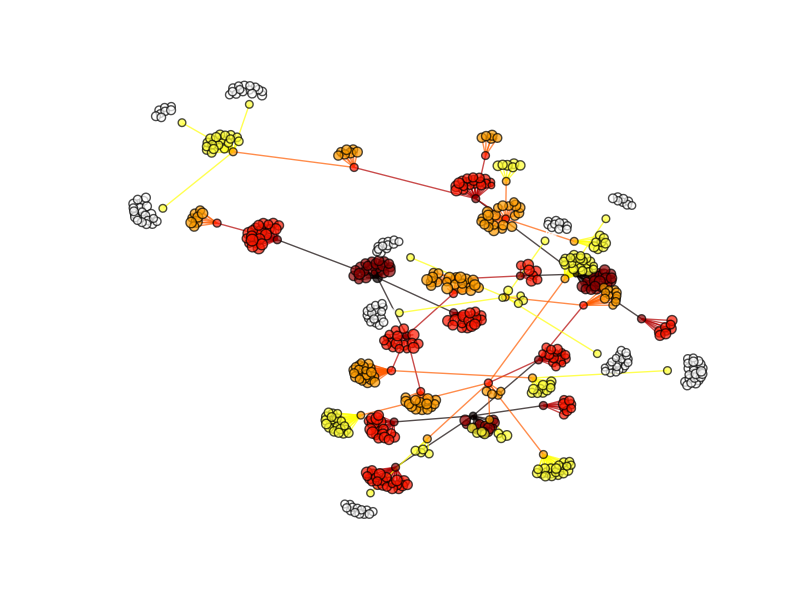
メタヒューリスティクスの数理
複雑な世界、単純な法則 ネットワーク科学の最前線
新ネットワーク思考―世界のしくみを読み解く