sofでグラフ(ネットワーク)を描くためのjavascriptライブラリを見つけたので調べていたら、twitterでCytoscapewebを教えてもらったので、cytoscape使い的にはそっちで色々試してからCytoscapewebで描画できるようにすれば効率的であることに気づき、自分のBlogのタグネットワークを描かせてみることにした。

が、色々つまづいて結局そこまでは至らなかったという。まず、networkxはutf8の属性含んだネットワークをgmlで出力仕様とするとエラーはいた。

しょうがないのでigraphでやるかと思ったらigraphの場合はネットワークを組み立てる場合には結構めんどくさかった（隣接行列から構築する場合には楽だけど）基本的に行列用意しておいて読み込ませるのはいいんだけど、sqlalchemyからオブジェクトをひっぱりつつネットワークを組み立てていくってのはnetworkxのほうがやりやすいようだ。 致命的だったのが、mac osxだとsaveしようとするとBus errorが出てセーブできなかった。

心が折れたので、igraphのプロットのスクリーンショット。

描かせたネットワークは僕のブログのエントリに入ってたタグ名をその頻度でノードの半径が大きくなるようにして、エッジは同じエントリに出現した場合（いわゆる共起）に貼るようにしたもの。

本当はこれをベースにして共起頻度の閾値を決めたり、ノードに最後に現れた日の情報を持たせて古いタグは透明度あげたりしようと思っているので、週末にでもSIFで出力してcytoscapeで綺麗にして適当なフォーマットでエクスポートしてcytoscapewebで見れるようにしてみよう。

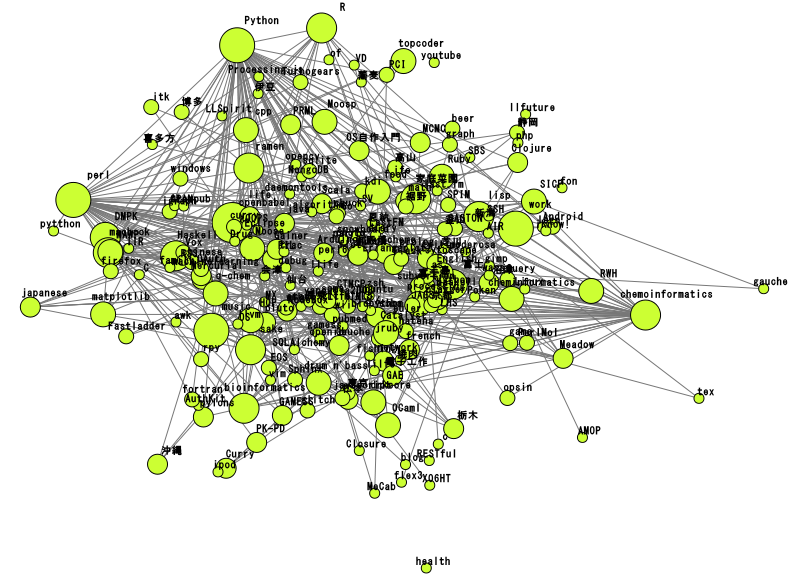
ちなみにpythonでigraphをいじるのは下のチュートリアルが良かった。

• Python Tutorial

日本語で書籍になっているのはこれ。

ネットワーク分析 (Rで学ぶデータサイエンス 8)
鈴木 努
共立出版 / ￥ 3,465 ( 2009-09-25 )

from database import db_session
from models import Entry, Tag
from math import log
import igraph

entries = db_session.query(Entry).filter(Entry.publish == 1).order_by(Entry.pubdate.desc()).all()

g=igraph.Graph()

all_tags = []

for entry in entries:
    tags = [tag for tag in entry.tags]
    i = 0
    for tag in tags:
        if tag.name not in all_tags:
            all_tags.append(tag.name)

taghash = dict([(tag,i) for i,tag in enumerate(all_tags)])
tag_count = [0] * len(all_tags)

g.add_vertices(len(all_tags)-1)
g.vs["name"] = all_tags

all_edges = []
for entry in entries:
    tags = [tag for tag in entry.tags]
    num_tags = len(tags)
    if num_tags > 1:
        for i in range(num_tags-1):
            itag = tags[i].name
            tag_count[taghash[itag]] += 1
            for j in range(i+1,num_tags):
                jtag = tags[j].name
                tag_count[taghash[jtag]] += 1
                edge = (taghash[itag],taghash[jtag])
                if edge not in all_edges:
                    all_edges.append(edge)
    else:
        tag_count[taghash[tags[0].name]] += 1

vsizes = [int(log(tc))*5 + 10 for tc in tag_count]

g.add_edges(all_edges)

layout = g.layout("kk")
g.vs["label"] = g.vs["name"]

igraph.plot(g,layout=layout, bbox = (800, 600), edge_color = "#777777",\
vertex_label_size=10, vertex_size=vsizes, vertex_color="#ccff33")
#g.write_gml("tag_network.gml")

MCSを求めるには比較したい二つの化合物のModular Productを求めて、それの最大クリーク探索をすればいい。

Modular Productとは

• 二つのグラフの属性の対応が同じノードが両方共隣接していてエッジの属性が同じ場合
• 二つのグラフの属性の対応が同じノードが両方共隣接していない場合

にエッジを張ったグラフ。

これを作ってあとはigraphの最大クリーク探索メソッドで

import openbabel as ob
from igraph import *

sm1 = 'OCC(N)=O'
sm2 = 'O=CC(N)=O'

obc = ob.OBConversion()
obc.SetInAndOutFormats('smi','smi')

source = ob.OBMol()      
obc.ReadString(source,sm1)
source_atoms = [a for a in ob.OBMolAtomIter(source)]

target = ob.OBMol()      
obc.ReadString(target,sm2)
target_atoms = [a for a in ob.OBMolAtomIter(target)]

pairs = []
for i in range(len(source_atoms)):
    for j in range(len(target_atoms)):
        if source_atoms[i].GetAtomicNum() == target_atoms[j].GetAtomicNum():
            pairs.append((source_atoms[i].GetIdx(),target_atoms[j].GetIdx()))

p = []
for x in range(len(pairs)-1):
    for y in range(x+1,len(pairs)):
        u = pairs[x]
        v = pairs[y]
        if u[0] != v[0] and u[1] != v[1]:
            sb = source.GetBond(u[0],v[0])
            tb = target.GetBond(u[1],v[1])
            if sb != None: sbo = sb.GetBondOrder()
            if tb != None: tbo = tb.GetBondOrder()

            if (sb == None and tb == None) or (sb != None and tb != None and sbo == tbo):
                p.append((pairs.index(u),pairs.index(v)))

g = Graph(p)
mc = g.largest_cliques()
for c in mc:
    print [pairs[i] for i in c]

実際にはline graph(エッジとノードを入れ替えたグラフ)のModular Productをもとめてクリーク探索したほうが計算量がかなり減るらしい。

が、今回はやっていない。

Handbook of Chemoinformatics Algorithms (Chapman & Hall/Crc Mathematical and Computational Biology)

Chapman & Hall / ￥ 8,895 ()
通常1～3週間以内に発送

Chemoinformatics and Computational Chemical Biology (Methods in Molecular Biology)

Humana Press / ￥ 14,386 ()
近日発売　予約可

igraphはRとPythonのbindingがあるのにチュートリアルがほとんどなさげなので、ネットワーク分析の本があると手っ取り早く知れて良い。

ネットワーク分析 (Rで学ぶデータサイエンス 8)
鈴木 努
共立出版 / ￥ 3,465 ()
在庫あり。

クリーク探索

こんなネットワークからクリークを探してみる

g <-matrix(c(0,1,1,0,1,0,0,1,0,1,0,0,0,1,1,1,0,1,1,1,0,0,
             0,1,0,1,1,1,1,0,1,1,0,1,0,0,0,1,1,1,0,0,0,1,
             0,1,0,0,0),nrow=7,ncol=7,byrow=TRUE) 
a <- graph.adjacency(g)
maximal.cliques(a)
[[1]]
[1] 0 1 2

[[2]]
[1] 1 6

[[3]]
[1] 0 2 4

[[4]]
[1] 2 3 4 5

[[5]]
[1] 3 6

追記 100818

Pythonの場合

a = [[0,1,1,0,1,0,0],
[1,0,1,0,0,0,1],
[1,1,0,1,1,1,0],
[0,0,1,0,1,1,1],
[1,0,1,1,0,1,0],
[0,0,1,1,1,0,0],
[0,1,0,1,0,0,0]]

g = GraphBase.Adjacency(a,mode=ADJ_UNDIRECTED)
g.maximal_cliques() # [(0, 1, 2), (1, 6), (0, 2, 4), (2, 3, 4, 5), (3, 6)]
g.largest_cliques() # [(2, 3, 4, 5)]