昨晩の夢にでてきた草むしりの草の名前だがオヒシバというらしい。根が強くて手だけではむしれない。

GH 草取りフォーク SF-12

石黒金属 / ()
在庫あり。

このフォークがあるとぐいっと引っ掛けて根っこごと引っこ抜けるので楽しい。昨日の朝一時間以上夢中で抜いてたらとうとう夢にまで登場した次第。

でも、丁寧にむしってても小さいのはどんどん生えてきてどうしようもないので、ホーも必要だろうということになった。

手打鋼付　立鎌ホー（大） 09010

/ ()

育つ雑草
鬼束ちひろ
ユニバーサルミュージック / ￥ 1,260 (2004-10-27)
在庫あり。

雨と仕事のタイミングがあわなくて二週間くらい放っといたら雑草が凄いことになってた。

パプリカと加茂茄子

トマトとゴーヤの花

草刈りすんのにいいのはないかな。

とりあえず、草刈りフォークを買ってみる。

GH 草取りフォーク SF-12

石黒金属 / ()
在庫あり。

早起きして、チャリで畑に行って草刈りする習慣をつける

富士サファリに行ってきた。

リスザルに餌やり。

サファリはナビカーとかいうのを借りた。キリンとシカの餌やりがついてる。シカセンベーはまぁどうでもいいけど、キリンに餌をあげられるのは良い。のそっと近づいてきてムシャッと食べるのね。あと舌の色が青っぽいというか黒っぽいというか。

ナビカーだとアスファルトを外れて、オフロードコースを走ることが出来る。ライオン、トラとかバイソンの間近まで接近できて迫力満点なのでお薦め（というか全然違う）。前日にライオンにバンパー噛まれたらしく、歯形が残っていた。

レストランのライオンのオムライス。作りが丁寧で驚いた。というより、写真と違いすぎると子供が泣くんだろうな。

帰り道で娘に何が一番良かったか聞いたら、「モルモットの抱っこ」とのこと。

数学読み物

フィボナッチのうさぎ―数学探険旅行
キース ボール
青土社 / ￥ 2,730 ()
在庫あり。

ISBNって誤り検出できるようになっているのね。あとバイナリプロトコルの話が楽しかった。

読み流した。

タオイズム。面白かった。

タオは笑っている (プラネタリー・クラシクス)
R・M・スマリヤン
工作舎 / ￥ 2,100 ()
在庫あり。

33の成功するヒッピーの話と44の「おわかりかな」が特に良かった。

それから、一通り読んでから2のタオの詩を読むのがよい。

• まがった人間が正しいことをしても結果は往々にして悪い
• 自分と自然を一つの連続体としてみる。
  • ligandとproteinもこのような思想で捉えることも多い
• 見ようとしても見えない 耳をすましても聞こえない しかしそれは無尽蔵である

昔、インフラ整備をしてた時に、よいインフラ整備のやりかたとは現場にインフラ整備のためにビジネスロジックが変更されているのを意識させないで、ただあるがままに流れた結果になることなのかなと思ったことがあって、それって、昔読んだ老子かなんかの良い政治とはみたいな話だなぁと。

ゴーヤの成長速度には驚く。

小さいまま、黄色くなってしまった。こういうのは種取りに使うといいらしい。

枝豆。少しモギって茹でてみたら美味しかったので、そろそろ全部収穫するか。

近所のホームセンターで秋用の茄子とかキュウリの苗が出回っているという情報を得たのでさっそくいったのだけど、モロヘイヤの苗しかおいてなかった。売ってるのはカインズのほうかな。

明日また行ってみる。

クリアランス

ファーマコキネティクス―演習による理解
杉山 雄一,山下 伸二,加藤 基浩
南山堂 / ￥ 6,300 ()
在庫あり。

設問1

CLr = Dose/AUC * fe = Dose/AUC * [排泄量]/Dose = [排泄量]/AUC

> data <- read.csv("/Users/kzfm/PK/pk35a.csv")
> attach(data)
> data
  Dose  AUC     e
a  200  7.3  71.9
b  400 15.3 128.0
c  800 34.3 217.0

> CLr <- e/AUC
> CLr
[1] 9.849315 8.366013 6.326531

> F <- 0.85
> QH <- 1.5
> QR <- 1.2
> GFR <- 0.12
> fb <- 0.2
> Vd <- 100

設問2

> CLtot <- Dose*0.85/AUC
> CLtot
[1] 23.28767 22.22222 19.82507
> CLh <- CLtot - CLr
> CLh
[1] 13.43836 13.85621 13.49854

解答では E = 1-F = CLh/Qhから求めてた。 BAと消化管の吸収性から肝クリアランスの見積もりも可能。

設問3

> data2 <- read.csv("/Users/kzfm/PK/pk35b.csv")
> data2
   ve   conc
a   5  0.194
b  10  0.404
c  20  0.863
d  50  2.480
e 100  5.540
f 200 12.000

> CLtot <- data2[,"ve"]/data2[,"conc"]
> CLtot
[1] 25.77320 24.75248 23.17497 20.16129 18.05054 16.66667

> CLr <- CLtot -13.5
> CLr
[1] 12.273196 11.252475  9.674971  6.661290  4.550542  3.166667

設問4

CLrはGFRと腎尿細管分泌クリアランスの和 CLr = (1-FR)(fb*GFR + CLrs) CLrs = CLr - fb*GFR

> CLrs <- CLr -fb*GFR*60
> CLrs
[1] 10.833196  9.812475  8.234971  5.221290  3.110542  1.726667

設問5

CLrs_uint = CLrs*QR/fb*(QR-CLrs)

> CLrs_uint <- CLrs*QR*60/(fb*(QR*60-CLrs))
> CLrs_uint
[1] 63.75927 56.80385 46.49241 28.14766 16.25495  8.84546

> e <- nls(CLrs_uint ~ Vmax/(Km+data2[,"conc"]*fb),start=list(Vmax=10,Km=10))
> e
Nonlinear regression model
  model:  CLrs_uint ~ Vmax/(Km + data2[, "conc"] * fb) 
   data:  parent.frame() 
   Vmax      Km 
23.2331  0.3267 
 residual sum-of-squares: 0.2010

Number of iterations to convergence: 12 
Achieved convergence tolerance: 2.395e-07 

設問6

省略というかわからん

設問7

省略というかわからん

クリアランス

ファーマコキネティクス―演習による理解
杉山 雄一,山下 伸二,加藤 基浩
南山堂 / ￥ 6,300 ()
在庫あり。

設問1

定常状態ではe*(-kelt) ~ Css_min/Css_maxであることを利用して

Css_avg = Css_max-Css_min/(ln(Css_max) - ln(Css_min))

> data <- read.csv("/Users/kzfm/PK/pk34.csv")
> data
     D Css_max Css_min    fe
a   60    14.1    9.55 0.082
b  120    22.2   14.80 0.098
c  300    45.0   30.50 0.076
d  600    90.8   62.30 0.090
e 1200   114.0   81.30 0.110
f 2400   146.0  105.00 0.091

> attach(data)
> Css_avg <- (Css_max - Css_min)/log(Css_max/Css_min)
> Css_avg
[1]  11.67764  18.25065  37.28122  75.65745  96.73056 124.37574

> plot(D,Css_avg,ylim=c(0,150))
> par(new=T)
> plot(D,Css_max,ylim=c(0,150),xlab="",ylab="",pch=2)
> par(new=T)
> plot(D,Css_min,ylim=c(0,150),xlab="",ylab="",pch=3)
> par(new=T)

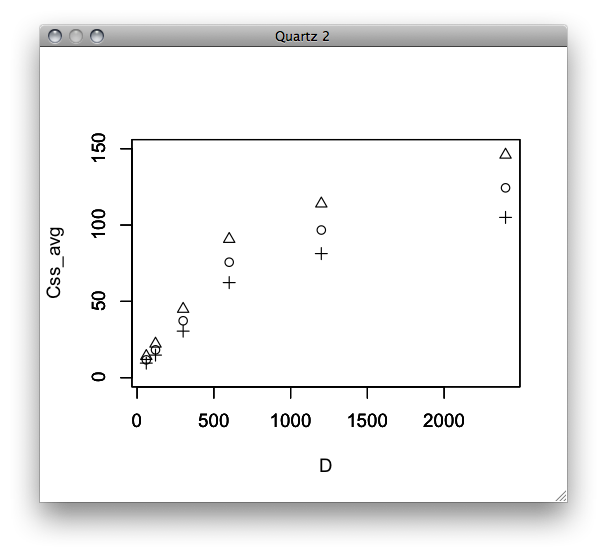
DoseとCpssに線形性がない。

設問2

定常状態の尿中排泄速度を定常状態の平均血中濃度で割る

> CLr <- (D/12*fe/60*1000)/Css_avg
> CLr
[1] 0.5851641 0.8949455 0.8494000 0.9913102 1.8952991 2.4388464

設問3

設問2からCLrが増加しており、これはfbの上昇、つまり血中蛋白結合の飽和が示唆される。

クリアランスとメカニズム

ファーマコキネティクス―演習による理解
杉山 雄一,山下 伸二,加藤 基浩
南山堂 / ￥ 6,300 ()
在庫あり。

設問1

> data <- read.csv("/Users/kzfm/PK/pk33.csv")
> data
  drag  dose      AUC   fe
a    A 1e+00    169.0 0.13
b    A 1e+01   1720.0 0.14
c    A 1e+02  22400.0 0.18
d    A 1e+03 530000.0 0.42
e    B 1e-02      2.4 0.17
f    B 1e-01     23.4 0.17
g    B 1e+00    167.0 0.19
h    B 1e+01    658.0 0.25

> attach(data)
> CLtot <- dose/AUC * 1000
> CLtot
[1]  5.917160  5.813953  4.464286  1.886792  4.166667  4.273504  5.988024 15.197568

> CLr <- CLtot * fe
> CLr
[1] 0.7692308 0.8139535 0.8035714 0.7924528 0.7083333 0.7264957 1.1377246 3.7993921

> CLh <- CLtot - CLr
> CLh
[1]  5.147929  5.000000  3.660714  1.094340  3.458333  3.547009  4.850299 11.398176

設問2

CLr = fb * GFR つまりfb = VLr/GFR

> GFR <- 8
> QH <- 60

> fb_a <- CLr[1]/8
> fb_b <- CLr[5]/8
> fb_a
[1] 0.09615385
> fb_b
[1] 0.08854167

CLh = (QH*fb*CLh_uint)/(QH+fb*CLh_uint)つまりCLh_uint=CLh*QH/(fb*(QH-CLh))

> CLh_uint_a <- CLh[1]*QH/(fb_a*(QH-CLh[1]))
> CLh_uint_a
[1] 58.56311
> CLh_uint_b <- CLh[5]*QH/(fb_b*(QH-CLh[5]))
> CLh_uint_b
[1] 41.44783

設問3

DrugA

CLrの投与量変化が見られないことからfbの変化はない。つまり投与量増加に伴うCLhの減少は CLh_uintの低下、つまり代謝過程の飽和

DrugB

投与量増加に伴い、CLh,CLrが増加。CLrの増加はfbの増加によるもので、これはつまり血中蛋白結合の 飽和をあらわしている。 肝固有クリアランスとの関係はなんとなく。

trunk(Rev: 3829)をDLしてきてコンパイル

svn co https://pymol.svn.sourceforge.net/svnroot/pymol/trunk pymol

freetypeがらみのヘッダーがないとかいうエラーがでてきたので

cd /usr/X11R6/include
sudo ln -s freetype2/freetype freetype

とsymbolic link張って解決

Bioinformatics Programming Using Python
Mitchell L. Model
Oreilly & Associates Inc / 5075円 ( 2009-12-23 )