クリアランス
ファーマコキネティクス―演習による理解設問1
定常状態ではe*(-kelt) ~ Css_min/Css_maxであることを利用して
Css_avg = Css_max-Css_min/(ln(Css_max) - ln(Css_min))
> data <- read.csv("/Users/kzfm/PK/pk34.csv")
> data
D Css_max Css_min fe
a 60 14.1 9.55 0.082
b 120 22.2 14.80 0.098
c 300 45.0 30.50 0.076
d 600 90.8 62.30 0.090
e 1200 114.0 81.30 0.110
f 2400 146.0 105.00 0.091
> attach(data)
> Css_avg <- (Css_max - Css_min)/log(Css_max/Css_min)
> Css_avg
[1] 11.67764 18.25065 37.28122 75.65745 96.73056 124.37574
> plot(D,Css_avg,ylim=c(0,150))
> par(new=T)
> plot(D,Css_max,ylim=c(0,150),xlab="",ylab="",pch=2)
> par(new=T)
> plot(D,Css_min,ylim=c(0,150),xlab="",ylab="",pch=3)
> par(new=T)
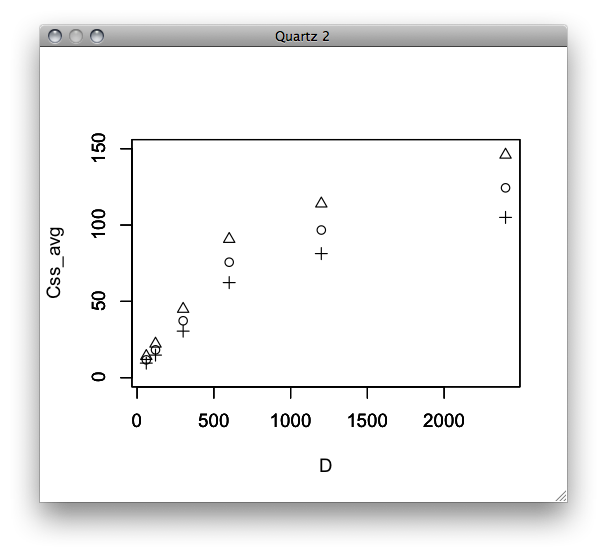
DoseとCpssに線形性がない。
設問2
定常状態の尿中排泄速度を定常状態の平均血中濃度で割る
> CLr <- (D/12*fe/60*1000)/Css_avg
> CLr
[1] 0.5851641 0.8949455 0.8494000 0.9913102 1.8952991 2.4388464
設問3
設問2からCLrが増加しており、これはfbの上昇、つまり血中蛋白結合の飽和が示唆される。