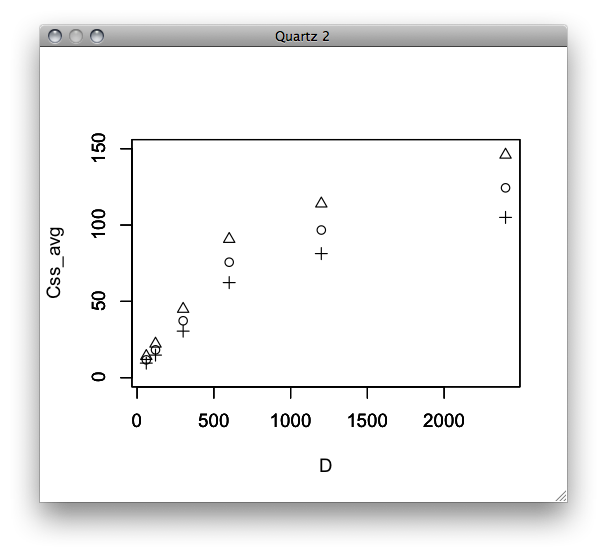
PBPKモデリング
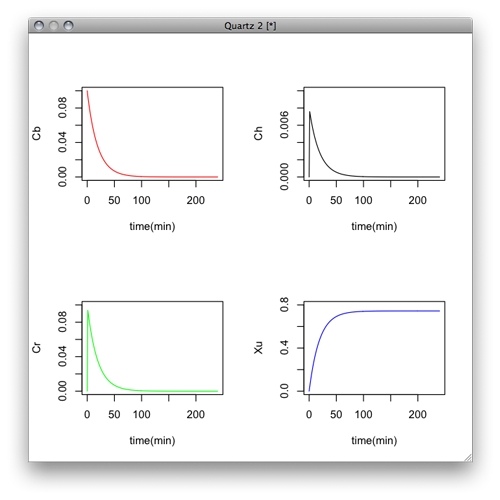
ファーマコキネティクス―演習による理解i.v.
library(odesolve)
params = c(Vh=44,Vr=8,Qh=58,Qr=45.6,Vsys=1000,Kph=1,Kpr=1,RB=1.5,fp=0.1,Fa=1,Vmax=1000,Km=0.1,GFR=6)
times=c(0,(1:240))
dydt <- function(t,y,p){
Vh <- p['Vh']
Vr <- p['Vr']
Qh <- p['Qh']
Qr <- p['Qr']
Vsys <- p['Vsys']
Kph <- p['Kph']
Kpr <- p['Kpr']
RB <- p['RB']
fp <- p['fp']
Fa <- p['Fa']
Vmax <- p['Vmax']
Km <- p['Km']
GFR <- p['GFR']
fb <- fp/RB
Cb <- (Qh*y[2]/Kph + Qr*y[3]/Kpr - Qh*y[1] - Qr*y[1])/Vsys
Ch <- (Qh*y[1] - (Vmax*fb*y[2]/Kph)/(Km+fb*y[2]/Kph) - Qh*y[2]/Kph)/Vh
Cr <- (Qr*y[1] - fb*GFR*y[1] - Qr*y[3]/Kpr)/Vr
Xu <- fb*GFR*y[1]
return(list(c(Cb,Ch,Cr,Xu)))
}
y <- lsoda(c(Cb=0.1,Ch=0.0,Cr=0.0,Xu=0.0),times,dydt,params)
par(mfrow=c(2,2))
plot(y[,1],y[,2],ylim=c(0,0.1),xlab="time(min)",ylab="Cb",type="l",col="red")
plot(y[,1],y[,3],ylim=c(0,0.01),xlab="time(min)",ylab="Ch",type="l",col="black")
plot(y[,1],y[,4],ylim=c(0,0.1),xlab="time(min)",ylab="Cr",type="l",col="green")
plot(y[,1],y[,5],ylim=c(0,0.8),xlab="time(min)",ylab="Xu",type="l",col="blue")
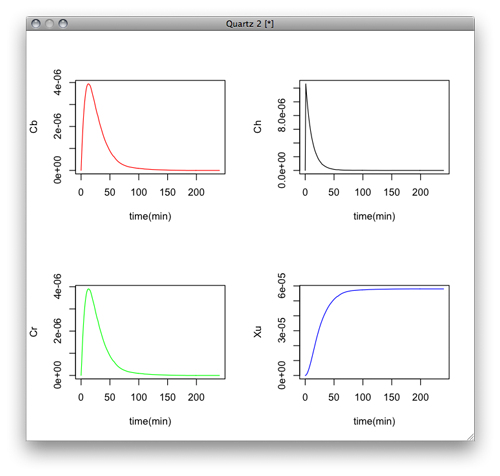
p.o.
params = c(Vh=44,Vr=8,Qh=58,Qr=45.6,Vsys=1000,Kph=1,Kpr=1,RB=1.5,fp=0.1,Fa=1,Vmax=1000,Km=0.1,GFR=6,Dose=0.1,ka=0.1)
times=c(0,(1:240))
dydt <- function(t,y,p){
Vh <- p['Vh']
Vr <- p['Vr']
Qh <- p['Qh']
Qr <- p['Qr']
Vsys <- p['Vsys']
Kph <- p['Kph']
Kpr <- p['Kpr']
RB <- p['RB']
fp <- p['fp']
Fa <- p['Fa']
Vmax <- p['Vmax']
Km <- p['Km']
GFR <- p['GFR']
Dose <- p['Dose']
ka <- p['ka']
fb <- fp/RB
Cb <- (Qh*y[2]/Kph + Qr*y[3]/Kpr - Qh*y[1] - Qr*y[1])/Vsys
Ch <- (Qh*y[1] - (Vmax*fb*y[2]/Kph)/(Km+fb*y[2]/Kph) - Qh*y[2]/Kph + Dose*ka*Fa*exp(-ka*t))/Vh
Cr <- (Qr*y[1] - fb*GFR*y[1] - Qr*y[3]/Kpr)/Vr
Xu <- fb*GFR*y[1]
return(list(c(Cb,Ch,Cr,Xu)))
}
y <- lsoda(c(Cb=0.0,Ch=0.0,Cr=0.0,Xu=0.0),times,dydt,params)
par(mfrow=c(2,2))
plot(y[,1],y[,2],xlab="time(min)",ylab="Cb",type="l",col="red")
plot(y[,1],y[,3],xlab="time(min)",ylab="Ch",type="l",col="black")
plot(y[,1],y[,4],xlab="time(min)",ylab="Cr",type="l",col="green")
plot(y[,1],y[,5],xlab="time(min)",ylab="Xu",type="l",col="blue")
母集団薬物データの解析 (統計科学選書)