デコンボリューション法が紹介されていたのできちんと理解しておきたいところ。
で、ちょっと調べたら古い論文がヒットした。
An algorithm and computer program for deconvolution in linear pharmacokinetics
fortranのコードが載っているのでpythonに移植すればいいやと軽く考えてたんだけど、go toで混乱している最中。if else 的なgo toは読みやすいんだけど、あっちいったりこっちいったりするのはちょっと辛い。
あとは式の内容ちゃんと理解してないのでコード追えないってのもあるが。 移植しながら論文の式の内容を理解していくつもりだったのだけどなかなか疲れる。
モーメント解析。AUCとAUMCをもとめるのにPKというライブラリを利用した。
ファーマコキネティクス―演習による理解library(PK)
time <- c(0.25, 0.5, 1, 2, 4, 6, 8, 10, 12, 16)
l_po_sol <- c(25.92, 33.75, 42.08, 28.81, 11.26, 4.24, 1.76, 0.59, 0.22)
l_po_tab <- c(1.3, 4.2, 11.33, 20.35, 20.15, 13.17, 6.66, 4.57, 1.81, 0.67)
l_iv <- c(91.21, 76.53, 61.46, 32.36, 11.9, 4.67, 2.15, 0.67, 0.25)
u_po_sol <- c(25.95, 33.75, 42.08, 28.81, 11.26)
u_po_tab <- c(11.33, 20.35, 20.15, 13.17)
u_iv <- c(91.21, 76.53, 61.46, 32.36, 11.9)
auc(time[1:9],l_po_sol,n.tail=3)
Estimation for a serial sampling design
AUC AUMC
observed 113.8863 1209.474
interpolated NA NA
infinity 140.1590 3005.290
auc(time,l_po_tab,n.tail=3)
Estimation for a serial sampling design
AUC AUMC
observed 106.8875 953.0328
interpolated NA NA
infinity 125.3667 1499.8264
auc(time[1:9],l_iv,n.tail=3)
Estimation for a serial sampling design
AUC AUMC
observed 193.5675 4534.682
interpolated NA NA
infinity 198.9328 5139.201
クリアランスは投与量をAUCでわればよい。
#CLtot = DOSE / AUC
0.1 / 198.9328 * 1000000 # = 502.6823
#Fsol = AUCpo(sol) / AUCiv
140.1590 / 198.9328 # 0.7045545
#Ftab = AUCpo(tab) / AUCiv
125.3667 / 198.9328 # 0.6301962
MRTはAUMCをAUCでわればよいはずなのだが、何かおかしい。演習の答えとあわん。
#MRT = AUMC / AUC
#Vss = CL * MRT
デコンボリューションはまたあとで。
昨晩AUMCがおかしかったのは、timeとconcの順番が逆だったという凡ミス。auc.completeでやれば明示的に指定できるのでこっちで書いてみた。
library(PK)
time <- c(0.25, 0.5, 1, 2, 4, 6, 8, 10, 12, 16)
l_po_sol <- c(25.92, 33.75, 42.08, 28.81, 11.26, 4.24, 1.76, 0.59, 0.22)
L_po_tab <- c(1.3, 4.2, 11.33, 20.35, 20.15, 13.17, 6.66, 4.57, 1.81, 0.67)
l_iv <- c(91.21, 76.53, 61.46, 32.36, 11.9, 4.67, 2.15, 0.67, 0.25)
l_po_sol_parm <- auc.complete(conc=c(0,l_po_sol), time=c(0,time[1:9]), n.tail=3)
l_po_tab_parm <- auc.complete(conc=c(0,l_po_tab), time=c(0,time), n.tail=3)
l_iv_parm <- auc.complete(conc=c(l_iv), time=c(time[1:9]), n.tail=3)
MRTをもとめる(AUMC / AUC)
> l_iv_parm$est[3,2]/l_iv_parm$est[3,1]
[1] 2.117064
> l_po_sol_parm$est[3,2]/l_po_sol_parm$est[3,1]
[1] 2.421341
> l_po_tab_parm$est[3,2]/l_po_tab_parm$est[3,1]
[1] 5.151322
これでうまくいきそう。
フィッティングのための初期値を求める。
ゾウの時間 ネズミの時間―サイズの生物学 (中公新書)t <- c(2.1, 4.1, 6.1, 8.1, 10.1, 14.1, 18.1, 22.1, 30.1, 45.2, 60.2,
120.3, 180.5, 241.8, 470, 948, 1423, 2187, 2831, 4305)
conc <- c(20.5, 17.5, 14.5, 12.5, 13.0, 12.0, 11.0, 9.1, 9.6, 5.6, 4.9,
3.2, 2.0, 1.8, 0.90, 0.85, 0.70, 0.45, 0.43, 0.39)
logc <- log(conc)
lm(logc[15:20] ~ t[15:20])
Call:
lm(formula = logc[15:20] ~ t[15:20])
Coefficients:
(Intercept) t[15:20]
-0.0399743 -0.0002441
exp(-0.0399)
[1] 0.9608855
beta <- function(t){exp(-0.0399743-t)}
ac <- conc[1:14] - beta(conc[1:14])
lm(ac ~ t[1:14])
Call:
lm(formula = ac ~ t[1:14])
Coefficients:
(Intercept) t[1:14]
13.19420 -0.06273
2,3exp式でフィッティングし、あてはめの良さをくらべる。
e2 <- nls(conc ~ a*exp(-alpha*t)+b*exp(-beta*t),
start=list(a=16,alpha=0.028,b=2,beta=0.000637))
e3 <- nls(conc ~ a*exp(-alpha*t)+b*exp(-beta*t)+c*exp(-gamma*t),
start=list(a=16,alpha=0.13,b=8.4,beta=0.0114,c=0.96,gamma=0.000239))
あてはめのよさは赤池の情報量基準で。Rの場合はAIC関数でよい。
AIC(e2) # [1] 56.79388
AIC(e3) # [1] 44.93942
というわけで、exp3式のほうがあてはまりがよい。
skip
微分方程式を解くためにodesolveを利用する。初期値の与えかたとか、ぐるぐる回していくイメージをつかむのに微妙に時間がかかったが、覚えてしまうと簡単な方程式を解かせたりシミュレーションするのには楽になる。
吸収過程を考えないコンパートメントモデル
library(odesolve)
params <- c(kel = 0.037)
times <- c(0,(1:40))
dydt <- function(t,y,p){
kel <- p['kel']
y <- -kel*y
list(c(y))
}
y <- lsoda(c(y = 8.6),times,dydt,params)
plot(y,ylab="Conc",xlab="time (hour)")
今度は吸収過程を考える。設問3は吸収速度定数を1/10にした時にどういう挙動を示すか。
params <- c(kel = 0.037,ka = 0.1, D = 5000, V = 580)
times <- c(0,(1:120))
dydt <- function(t,y,p){
kel <- p['kel']
ka <- p['ka']
D <- p['D']
V <- p['V']
y <- ka * (D/V) * exp(-ka*t) -kel*y
list(c(y))
}
y <- lsoda(c(y = 0),times,dydt,params)
params2 <- c(kel = 0.037,ka = 0.01, D = 5000, V = 580)
y2 <- lsoda(c(y = 0),times,dydt,params2)
plot(y,ylim=c(0,6),ylab="Conc",xlab="time(hour)")
par(new=T)
plot(y2,ylim=c(0,6),axes=F,xlab="",ylab="")
今回バイオアバイラビリティ(F)を1とおいているが、これを変化させた時の挙動も気になるのでやってみた。設問の式にFを組み込んでF=0.1とした時の結果
dydt2 <- function(t,y,p){
kel <- p['kel']
ka <- p['ka']
D <- p['D']
V <- p['V']
F <- p['F']
y <- ka * (D/V) * F * exp(-ka*t) -kel*y
list(c(y))
}
params3 <- c(kel = 0.037,ka = 0.1, D = 5000, V = 580, F = 0.1)
y3 <- lsoda(c(y = 0),times,dydt2,params3)
plot(y2,ylim=c(0,3),axes=F,xlab="time(hour)",ylab="Conc")
par(new=T)
plot(y3,ylim=c(0,3),axes=F,xlab="",ylab="")
あーなるほど、そうだよなぁと一人で妙に納得したのであった。
18052009 DMPK
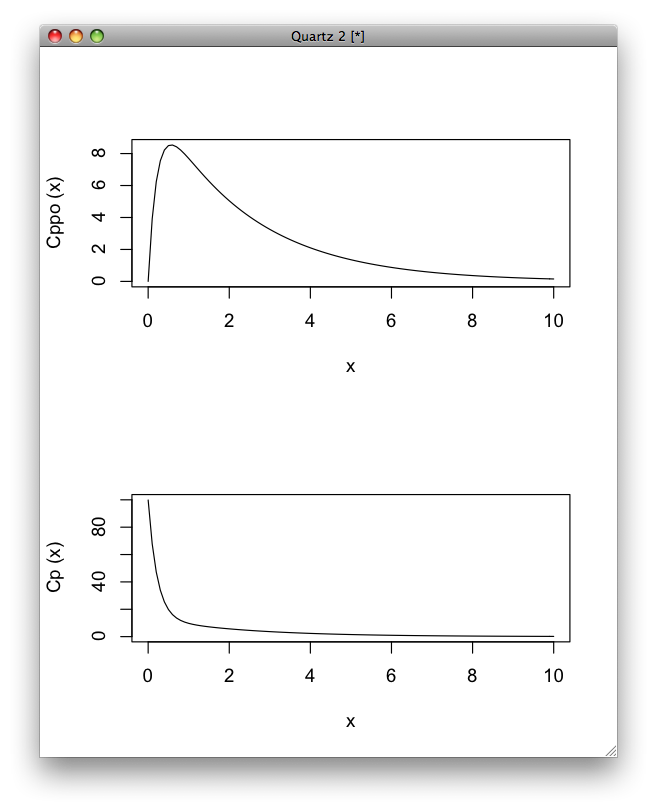
演習の本をRでこなしていくことにした。
β層の消失速度をもとめて、それを用いてα層の消失速度を決定する。
分子薬物動態学t <- c(1,2,3,6,13,23,30,39,49)
c <- c(68.2, 51.1, 43.2, 34.0, 18.3, 11.5, 10.7, 10.6, 6.78)
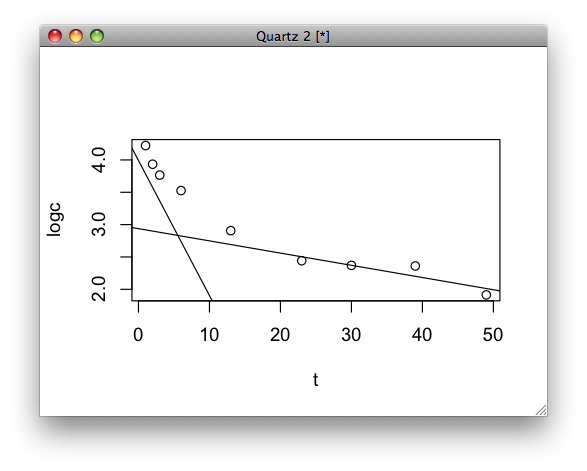
23時間からの濃度からβ層の消失速度を求める
logc <- log(c)
result <- lm(logc[6:9] ~ t[6:9])
coef(result)
(Intercept) t[6:9]
2.93770720 -0.01888941
β層の消失速度が決まったので、次は23時間までの濃度からβ層の寄与を引いた濃度からα層の消失速度を決定する
beta <- function(t){exp(2.937707-0.01889*t)}
alogc <- c[1:5] - beta(t)[1:5]
aresult <- lm(alogc ~ t[1:5])
これでα層β層それぞれの消失速度がもとまる
result
Call:
lm(formula = logc[6:9] ~ t[6:9])
Coefficients:
(Intercept) t[6:9]
2.93771 -0.01889
aresult
Call:
lm(formula = alogc ~ t[1:5])
Coefficients:
(Intercept) t[1:5]
3.9916 -0.2088
求めるモデルは
exp(3.9916-0.2088*t)+exp(2.937707-0.01889*t)
ラフに求めたA,B,alpha,betaを初期値として最小自乗法でフィッティングを行う。1exp,2expでやってみて、どっちのあてはまりがよいか考える
t <- c(1,2,3,6,13,23,30,39,49)
conc <- c(68.2, 51.1, 43.2, 34.0, 18.3, 11.5, 10.7, 10.6, 6.78)
dat <- data.frame(conc,t)
result <- nls(conc ~ a*exp(-alpha*t),start=list(a=50,alpha=0.045))
summary(result)
Formula: conc ~ a * exp(-alpha * t)
Parameters:
Estimate Std. Error t value Pr(>|t|)
a 63.26990 5.39879 11.719 7.45e-06 ***
alpha 0.08359 0.01777 4.706 0.00219 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.608 on 7 degrees of freedom
Number of iterations to convergence: 14
Achieved convergence tolerance: 7.74e-06
f <- function(t){63.2699*exp(-0.0836*t)}
plot(f,0,50,xlim=c(0,50),ylim=c(0,70),xlab="Time",ylab="Conc")
par(new=T)
plot(t,conc,xlim=c(0,50),ylim=c(0,70),axes=F,xlab="",ylab="")
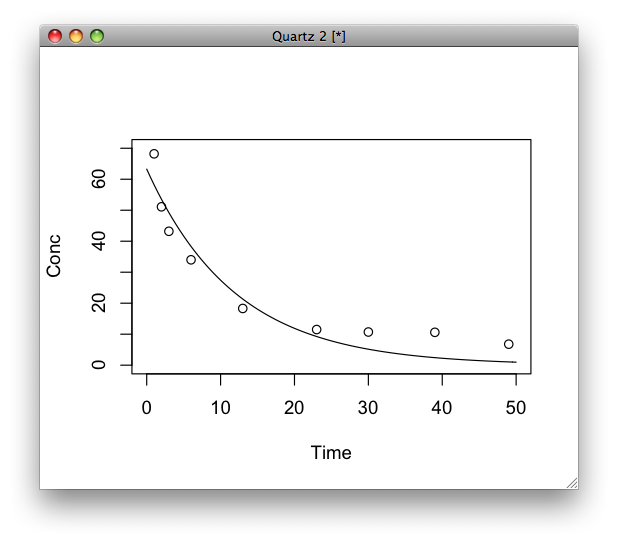
一層の消失モデルだと特に遅い時間の当てはめが悪い。ちなみにRだとAIC関数使えば適合度がでる。
t <- c(1,2,3,6,13,23,30,39,49)
conc <- c(68.2, 51.1, 43.2, 34.0, 18.3, 11.5, 10.7, 10.6, 6.78)
dat <- data.frame(conc,t)
result <- nls(conc ~ a*exp(-alpha*t)+b*exp(-beta*t),start=list(a=50,alpha=0.277,b=20,beta=0.0198))
summary(result)
f <- function (t){55.75*exp(-0.3769*t)+29.157*exp(-0.03189*t)}
plot(f,0,50,xlim=c(0,50),ylim=c(0,70),xlab="Time",ylab="Conc")
par(new=T)
plot(t,conc,xlim=c(0,50),ylim=c(0,70),axes=F,xlab="",ylab="")
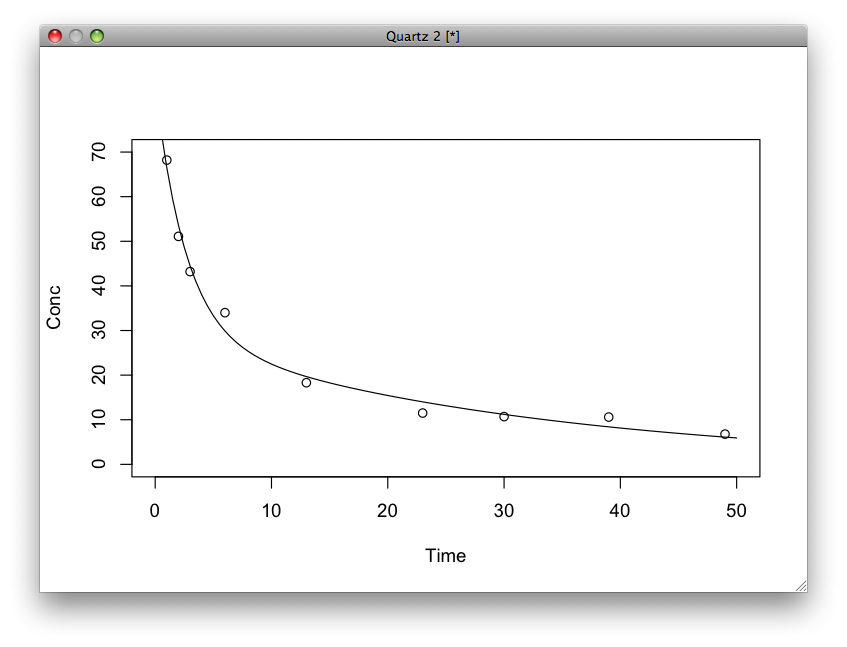
プロットするときにpar関数で上書きするのと、xlim,ylimを明示して軸をきちんとそろえつつ、目盛やタイトルを上書きして重ねないように気をつける。
ivivcというパッケージを発見。PKfitでkelとかVdを求めておけばこれで対話的に色々（というかルーチーンワークが）できるらしい。
demoのflashも用意されている。
****************************************************************************
* *
* ivivc *
* v 0.1.4 *
* *
* In vitro-in vivo correlation (IVIVC) is defined as the correlation *
* between in vitro drug dissolution and in vivo drug absorption. *
* This package is used to develop and validate an IVIVC model. *
* The following steps wii be conducted as follows: *
* ->1: Input/Edit In Vivo Absorption Data: IV, Oral solution or IR drug *
* ->2: Develop an IVIVC Model: Fitting IV, Oral solution or IR drug *
* ->3: Input/Edit In Vitro Dissoution Data and *
* In Vivo absorption Data: ER drug with Different Release Rates *
* ->4: Develop an IVIVC Model: Model Dependent Method *
* ->5: Evaluate an IVIVC model: Prediction Error *
* *
* Please type 'run()' to get started. *
* *
****************************************************************************
runしてdemoするとなんか一瞬で終わる。
Rでここまでのワークフローを対話的にやらすパッケージってのは自由度が少ない気もするが、あとでまた。
とりあえずPKfitをいじろうと思ってるんだけど、pdfのマニュアルがいい加減すぎるんだよね。
12052009 chemoinformatics DMPK
はじめて読むならこれがお薦めか。ケモインフォマティクスな僕にとってはある程度数式とか統計の話がくっついていたほうが、知識と照らし合わせながら覚えていけるので分かりやすかった。
ちょっと7章だけプロットしてみた。
はじめての薬物速度論Cp <- function(t){86.22 * exp(-4.55 * t) + 13.63 * exp(-0.438 * t)
Cppo <- function(t){456700/(9128*(4.567-0.438)) * (exp(-0.438 * t) - exp(-4.567 * t))}
par(mfrow = c(2,1))
plot(Cppo,0,10)
plot(Cp,0,10)
演習の多そうなこっちもやっとくべきか。