1. SUMMER OF LOVE,10. 七色ギャングスターが良い。

eREVEST
ゲッカンプロボーラー
インディーズ・メーカー / ￥ 2,300 (2009-07-08)
近日発売　予約可

little bootsは、どうなんだろ?若干流行ものな香りもするような。

Hands
Little Boots
Warner Music / ￥ 2,298 (2009-06-08)
在庫あり。

「天井の穴」

天井が透けていて、上に広がる世界が(既に)見えてるか？、または透けてないくて、開けた先がブルーオーシャンっぽいのかとかそういう、天井の不透明度的なことも重要な気がする。

あと、天井の強度の弱いポイントを探すとか。

女性杜氏の作らしい。

ぶっちゃけ、女性かどうかは関係ないけど。

ちょっと香りが気になったのと、若干くどく感じた。まぁ先週は吉田蔵の純米飲んでたので、そのせいもあるかもしれないけど。

Cation-πってどのくらい安定化すんだろうか?と思っていたので計算してみる。

RCSBを適当にあさって見つけた、1R9LのBETとTRP188を切り出してモデル化する。

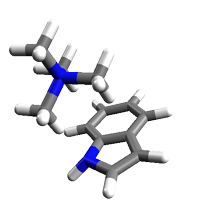
で、GAMESSで計算。

最初は6-31G+(d,p)で最適化しようと思ったのだけど、macbookだと全然終わらん。なのでSTO3Gでいいやと。TRPは無駄に計算量が増えるのだけどPHE,TYRあたりでモデル化できるのであればmacbookでも6-31G+(d,p)で計算できるような気がする。

          ------------------------------------
          RESULTS OF KITAURA-MOROKUMA ANALYSIS
          ------------------------------------

                                         HARTREE    KCAL/MOLE
 ELECTROSTATIC ENERGY             ES=   -0.011414      -7.16
 EXCHANGE REPULSION ENERGY        EX=    0.008788       5.51
 POLARIZATION ENERGY              PL=   -0.001679      -1.05
 CHARGE TRANSFER ENERGY           CT=   -0.007053      -4.43
 HIGH ORDER COUPLING ENERGY      MIX=    0.000166       0.10
 TOTAL INTERACTION ENERGY,   DELTA-E=   -0.011193      -7.02

水素結合と同じくらいの強さかな。

以下、STO-3Gで構造最適化した座標を使ってつくったインプット

 $BASIS GBASIS=STO NGAUSS=3 NDFUNC=1 $END
 $CONTRL SCFTYP=RHF RUNTYP=MOROKUMA MAXIT=200 ICHARG=1 MULT=1 $END
 $MOROKM IATM(1)=17 ICHM(1)=1 $END

 $DATA
W188_BET.out
C1
N      7.0    26.56861  22.88472  72.47206
C      6.0    25.05591  23.05763  72.38527
C      6.0    27.18276  23.04159  71.08205
C      6.0    27.14794  23.94295  73.40648
C      6.0    26.89124  21.49601  73.01604
H      1.0    24.65761  22.29324  71.71973
H      1.0    24.84300  24.05067  71.99229
H      1.0    26.95089  24.04166  70.71972
H      1.0    26.73892  22.29197  70.42917
H      1.0    28.26387  22.89551  71.15590
H      1.0    26.89847  24.92550  73.00913
H      1.0    28.22884  23.81270  73.44995
H      1.0    26.70726  23.81001  74.39332
H      1.0    26.46855  20.75492  72.33939
H      1.0    26.44825  21.40230  74.00640
H      1.0    27.97398  21.38820  73.06968
H      1.0    24.63622  22.94695  73.38408
C      6.0    30.61324  20.49644  72.40614 
C      6.0    30.47183  21.03406  71.19420 
C      6.0    30.79531  21.59051  73.36029 
C      6.0    30.75216  22.77934  72.62888 
C      6.0    31.00908  21.63948  74.74382 
N      7.0    30.43745  22.45766  71.27884 
C      6.0    30.92671  24.02761  73.23103 
C      6.0    31.18435  22.86580  75.34238 
C      6.0    31.14962  24.05129  74.58925 
H      1.0    30.33993  20.55500  70.23268
H      1.0    31.04481  20.72825  75.32842
H      1.0    30.86231  23.00634  70.52231
H      1.0    30.90815  24.93911  72.64846
H      1.0    31.36065  22.92555  76.40870
H      1.0    31.30378  24.99933  75.08996
H      1.0    30.61446  19.44515  72.64676 
 $END

すぐできる 量子化学計算ビギナーズマニュアル (KS化学専門書)

講談社 / ￥ 3,360 ()
在庫あり。

集合知プログラミングの著者が新しい本を出すみたい。

Programming the Semantic Web
Toby Segaran
Oreilly & Associates Inc / 3446円 ( 2009-07 )

コードはpythonなのかな。 ちょっと気になる。

仕事として.NETの開発をやるときに、C#はあんま気乗りがせんのう、IronPythonでやりたいなぁとつぶやいたら、

F#

という声が聞こえた。

あーF#もありか、と思ってしまったのであった。

Ocamlか。

プログラミング in OCaml ~関数型プログラミングの基礎からGUI構築まで~
五十嵐 淳
技術評論社 / ￥ 2,814 ()
在庫あり。

ボーナスが出るのでさらに本を。

アニマルでPPKをやれると色々良い気がする。

母集団薬物データの解析 (統計科学選書)
矢船 明史
朝倉書店 / 3045円 ( 2004-02 )

Rのnlmeも同じ作者っぽいので、これを買っても役に立つだろう的な期待感から。

Mixed-Effects Models in S and S-PLUS (Statistics and Computing)
José Pinheiro
Springer / 2859円 ( 2009-04-15 )

上司の薦め。いい本らしいので、読んでみる。

Drug-like Properties: Concepts, Structure Design and Methods: from ADME to Toxicity Optimization
Edward Kerns
Academic Press / 9726円 ( 2008-02-19 )

学会に参加するなら、発表する方向で臨まないと得られるものがないよね。

国際学会English―挨拶・口演・発表・質問・座長進行
C.S.ラングハム
医歯薬出版 / 2625円 ( 2007-04 )

面白い。

はじめての現代数学 (数理を愉しむ)シリーズ (ハヤカワ文庫NF)
瀬山 士郎
早川書房 / ￥ 777 ()
在庫あり。

現代数学を観光気分で満喫する本。小難しい数式とか証明はほとんどでてこないので、気張らずに読めた。

「モノ」から「コト」へ。

無限の大小とかトポロジーの話とか面白かったが、ゲーデルの不完全定理がいまいちつかめなかった(が、チューリングの停止問題は理解できるんだけど)。

文庫本なので鞄にしのばせておくとよい。

ローレンツのついでにgumowski

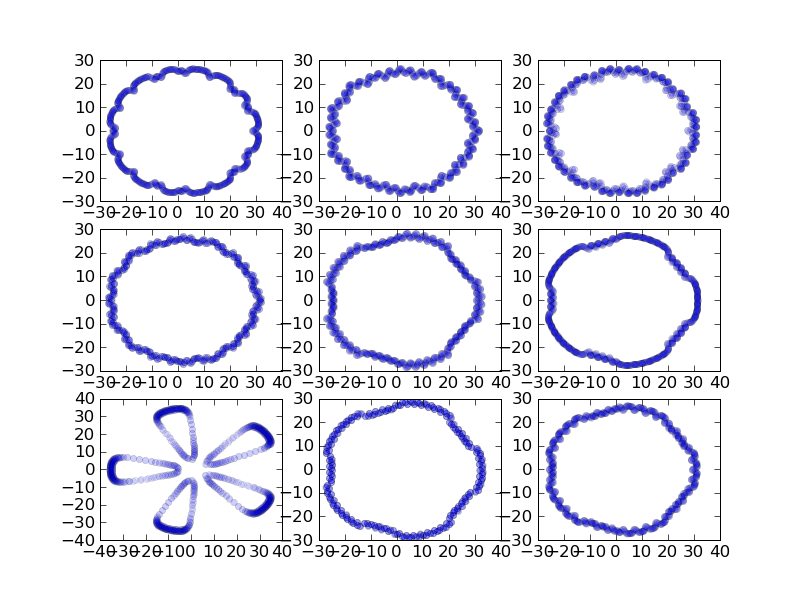
class Gumowski:
    "Gumowski-Mira Map"
    def __init__(self, x0, y0, a):
        self.x0 = x0; self.y0 = y0
        self.a  = a;

    def f(self,x):
        return self.a*x + 2*(1-self.a)*x**2/(1+x**2)

    def calc(self, n):
        dat = []
        x,y = self.x0, self.y0
        for i in range(n):
            nx = y  + self.f(x)
            ny = -x + self.f(nx)
            dat.append([nx,ny])
            x,y = nx,ny
        return dat

if __name__ == "__main__":
    from pylab import *
    from random import random
    n = 3
    for i in range(n*n):
        p = str(n) + str(n) + str(i+1)
        subplot(p)
        a = random() * 0.1 + 0.3
        gumow = Gumowski(20, 20, a)
        dat = gumow.calc(1000)
        x = [d[0] for d in dat]
        y = [d[1] for d in dat]
        plot(x,y,'bo', alpha=0.1,ms=5)

    savefig("gumow.png")

どう書くより。

python+matplotlibで。

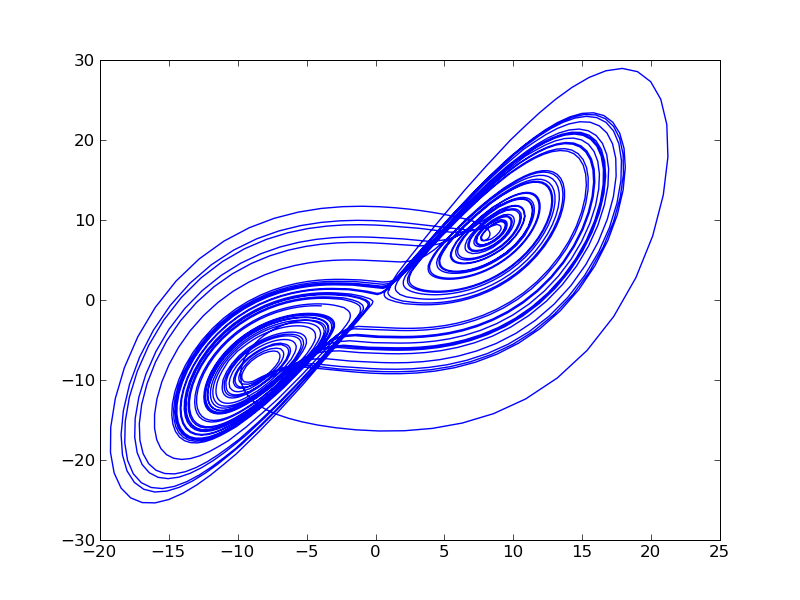
class Lorenz:
    "Lorenz attractor"
    def __init__(self, x0, y0, z0, p, r, b, dt):
        self.x0 = x0; self.y0 = y0; self.z0 = z0
        self.p  = p;  self.r  = r;  self.b  = b
        self.dt = dt

    def calc(self, n):
        dat = []
        x,y,z = self.x0, self.y0, self.z0
        for i in range(n):
            dx = (-1 * self.p * x + self.p * y) * self.dt
            dy = (-x * z + self.r * x - y) * self.dt
            dz = (x * y - self.b * z) * self.dt
            x += dx; y += dy; z += dz
            dat.append([x,y,z])
        return dat

if __name__ == "__main__":
    from pylab import *
    lorenz = Lorenz(1.0, 1.0, 1.0, 10.0, 28.0, 8.0/3.0, 0.01)
    dat = lorenz.calc(5000)
    x = [d[0] for d in dat]
    y = [d[1] for d in dat]
    plot(x,y)
    savefig("lorenz.png")