Let Over Lambdaを買っているヒトはミンスキー博士も買っているらしいとamazonに教えられてちょっと興味を持った。

ミンスキー博士の脳の探検 ―常識・感情・自己とは―
Marvin Minsky
共立出版 / ￥ 4,725 ()
在庫あり。

もちろんlolも欲しいんだが、まだ買ってない。

LET OVER LAMBDA Edition 1.0
ダグ ホイト
エスアイビーアクセス / ￥ 3,360 ()
在庫あり。

プログラミング in OCamlは今日届いた。来週、夏休みなので読む。

プログラミング in OCaml ~関数型プログラミングの基礎からGUI構築まで~
五十嵐 淳
技術評論社 / ￥ 2,919 ()
在庫あり。

脳内のレセプターと薬物の結合のシミュレーション

ファーマコキネティクス―演習による理解
杉山 雄一,山下 伸二,加藤 基浩
南山堂 / ￥ 6,300 ()
在庫あり。

odesolveで血中濃度が時間依存的に減少するとき(時間の関数になっているとき)どういう風に書けばいいのか悩んだが

Cp <- dose/mwt*(50*exp(-0.1*t) + 125*exp(-0.025*t))

とtそのまま使えることがわかったので解決

library(odesolve)
times=c(0,(1:120))
params = c(fb=0.2,mwt=250, Kp=8.0, kon=2,koff=0.2,Rt=1,Vt=1,Q=1,dose=0.2)

dydt <- function(t,y,p){
fb <- p['fb']
Kp <- p['Kp']
kon <- p['kon']
koff <- p['koff']
Rt <- p['Rt']
Vt <- p['Vt']
Q <- p['Q']
dose <- p['dose']
mwt <- p['mwt']

Cp <- dose/mwt*(50*exp(-0.1*t) + 125*exp(-0.025*t))
Ct <- (Q*(Cp-y[1]/Kp)-kon*fb*y[1]/Kp*Rt*(1-y[2])+koff*Rt*y[2])/Vt
PHAI <- kon*fb*y[1]/Kp*(1-y[2])-koff*y[2]
return(list(c(Ct,PHAI)))
}

y <- lsoda(c(Ct=0.0,PHAI=0.0),times,dydt,params)

y02 <- y
params = c(fb=0.2,mwt=250, Kp=8.0, kon=2,koff=0.2,Rt=1,Vt=1,Q=1,dose=1)
y <- lsoda(c(Ct=0.0,PHAI=0.0),times,dydt,params)
y1 <- y
params = c(fb=0.2,mwt=250, Kp=8.0, kon=2,koff=0.2,Rt=1,Vt=1,Q=1,dose=5)
y <- lsoda(c(Ct=0.0,PHAI=0.0),times,dydt,params)
y5 <- y

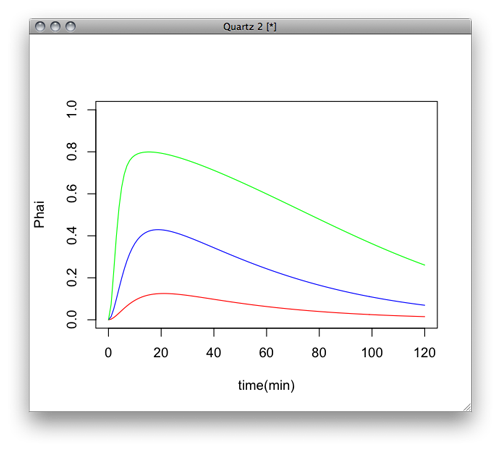
plot(y02[,1],y02[,3],ylim=c(0,1.0),xlab="time(min)",ylab="Phai",type="l",col="red")
par(new=T)
plot(y1[,1],y1[,3],ylim=c(0,1.0),xlab="",ylab="",axes=F,type="l",col="blue")
par(new=T)
plot(y5[,1],y5[,3],ylim=c(0,1.0),xlab="",ylab="",axes=F,type="l",col="green")

plot(y2[,2],y5[,3],ylim=c(0,1.0),xlab="Cb",ylab="Phai",type="l",col="red")

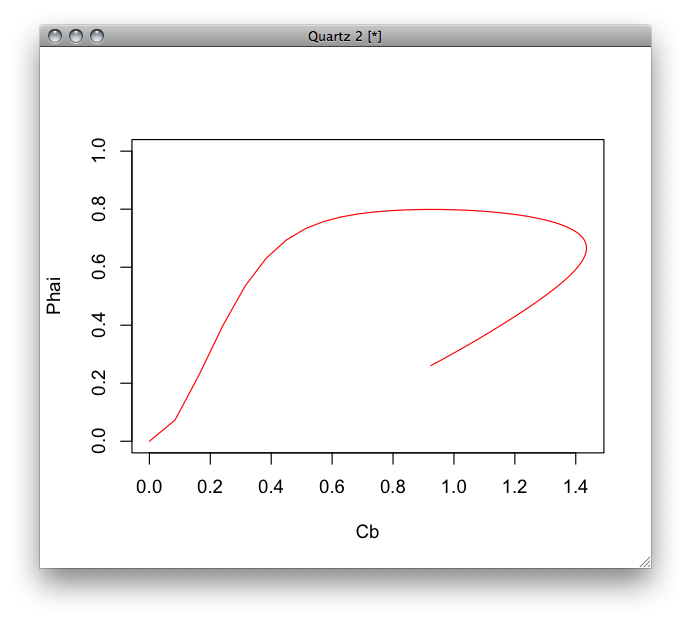
ヒステリシスがみられる

野菜の育つ過程をもとに美味しい野菜とは何かを考える。「健康に育った野菜は美味い」という前提に立ちすぎな気もするが。

おいしい野菜の見分け方
徳岡邦夫,西村和雄,山口規子(写真)
バジリコ / ￥ 1,575 ()
在庫あり。

• 葉脈
• 葉の出方
• ヘタの形

根菜は成長輪が均等なもの(どこかで化成肥料が入ると急速に成長するため均等でなくなる)

• 里芋
• しょうが

ひげ根の出る位置も重要

• 人参
• 大根

ねぎはらっきょうのように根元がふくらんでいるもの

ゴーヤーは白っぽいもの（あまり緑にならないうちに収穫しよう）

葉物は葉っぱの出方が重要なので、茎のそろい方に注意

今度、菜園になんか植えた時に化成肥料の有無で比較してみよう

すっきりしていて、今の時期には丁度いいかも。

美味い。しかも2.1K也

PBPKモデリング

ファーマコキネティクス―演習による理解
杉山 雄一,山下 伸二,加藤 基浩
南山堂 / ￥ 6,300 ()
在庫あり。

i.v.

library(odesolve)
params = c(Vh=44,Vr=8,Qh=58,Qr=45.6,Vsys=1000,Kph=1,Kpr=1,RB=1.5,fp=0.1,Fa=1,Vmax=1000,Km=0.1,GFR=6)
times=c(0,(1:240))

dydt <- function(t,y,p){
Vh <- p['Vh']
Vr <- p['Vr']
Qh <- p['Qh']
Qr <- p['Qr']
Vsys <- p['Vsys']
Kph <- p['Kph']
Kpr <- p['Kpr']
RB <- p['RB']
fp <- p['fp']
Fa <- p['Fa']
Vmax <- p['Vmax']
Km <- p['Km']
GFR <- p['GFR']
fb <- fp/RB
Cb <- (Qh*y[2]/Kph + Qr*y[3]/Kpr - Qh*y[1] - Qr*y[1])/Vsys
Ch <- (Qh*y[1] - (Vmax*fb*y[2]/Kph)/(Km+fb*y[2]/Kph) - Qh*y[2]/Kph)/Vh
Cr <- (Qr*y[1] - fb*GFR*y[1] - Qr*y[3]/Kpr)/Vr
Xu <- fb*GFR*y[1]
return(list(c(Cb,Ch,Cr,Xu)))
}

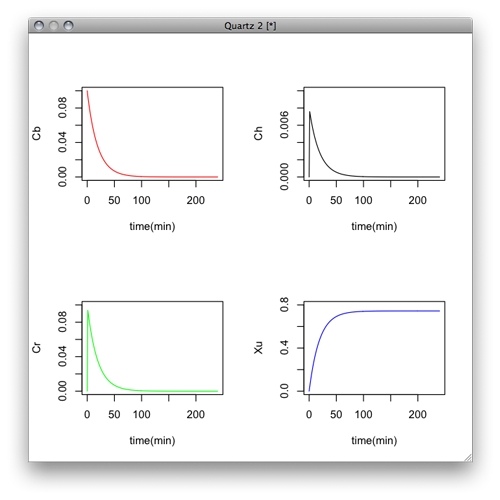
y <- lsoda(c(Cb=0.1,Ch=0.0,Cr=0.0,Xu=0.0),times,dydt,params)

par(mfrow=c(2,2))
plot(y[,1],y[,2],ylim=c(0,0.1),xlab="time(min)",ylab="Cb",type="l",col="red")
plot(y[,1],y[,3],ylim=c(0,0.01),xlab="time(min)",ylab="Ch",type="l",col="black")
plot(y[,1],y[,4],ylim=c(0,0.1),xlab="time(min)",ylab="Cr",type="l",col="green")
plot(y[,1],y[,5],ylim=c(0,0.8),xlab="time(min)",ylab="Xu",type="l",col="blue")

p.o.

params = c(Vh=44,Vr=8,Qh=58,Qr=45.6,Vsys=1000,Kph=1,Kpr=1,RB=1.5,fp=0.1,Fa=1,Vmax=1000,Km=0.1,GFR=6,Dose=0.1,ka=0.1)
times=c(0,(1:240))

dydt <- function(t,y,p){
Vh <- p['Vh']
Vr <- p['Vr']
Qh <- p['Qh']
Qr <- p['Qr']
Vsys <- p['Vsys']
Kph <- p['Kph']
Kpr <- p['Kpr']
RB <- p['RB']
fp <- p['fp']
Fa <- p['Fa']
Vmax <- p['Vmax']
Km <- p['Km']
GFR <- p['GFR']
Dose <- p['Dose']
ka <- p['ka']
fb <- fp/RB
Cb <- (Qh*y[2]/Kph + Qr*y[3]/Kpr - Qh*y[1] - Qr*y[1])/Vsys
Ch <- (Qh*y[1] - (Vmax*fb*y[2]/Kph)/(Km+fb*y[2]/Kph) - Qh*y[2]/Kph + Dose*ka*Fa*exp(-ka*t))/Vh
Cr <- (Qr*y[1] - fb*GFR*y[1] - Qr*y[3]/Kpr)/Vr
Xu <- fb*GFR*y[1]
return(list(c(Cb,Ch,Cr,Xu)))
}

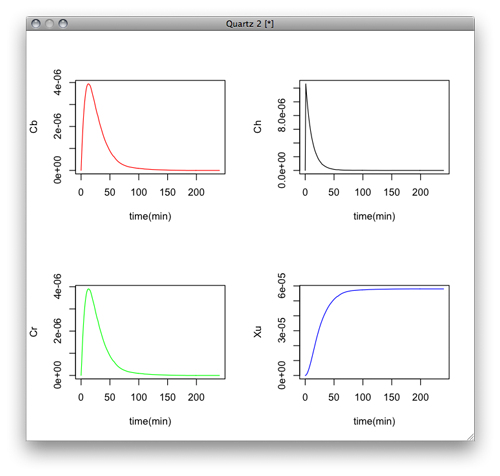
y <- lsoda(c(Cb=0.0,Ch=0.0,Cr=0.0,Xu=0.0),times,dydt,params)

par(mfrow=c(2,2))
plot(y[,1],y[,2],xlab="time(min)",ylab="Cb",type="l",col="red")
plot(y[,1],y[,3],xlab="time(min)",ylab="Ch",type="l",col="black")
plot(y[,1],y[,4],xlab="time(min)",ylab="Cr",type="l",col="green")
plot(y[,1],y[,5],xlab="time(min)",ylab="Xu",type="l",col="blue")

kdi(今度行く)

• エリミな気分 : 再移転後の「王様のカレー」
• 酒のいけたに
• 静岡道楽手帖 山正＠沼津市
• 鏡花水月-weblog::手打ちそば　ながいけ

itk(行ってきた)

• 創作居酒屋「縁」えにし沼津

縁にて

• 作
• 御湖鶴
• 石鎚　夏の吟醸
• 手取川　大吟醸
• 新亀　ひこ孫

料理は前菜として出された三種盛りとイサキの塩焼きが美味しかった。また今度行く。

薬物動態解析と統計の基礎から始まる概論的な読み物。

母集団薬物データの解析 (統計科学選書)
矢船 明史,石黒 真木夫,赤池 弘次
朝倉書店 / ￥ 3,045 ()

1. 序論
2. 薬物動態解析の概略
3. 統計理論の概略
4. 情報量規準
5. 母集団薬物動態解析
6. 血液中薬物濃度推移のベイズ推定
7. おわりに

1-4の概略はまとまっていてわかりやすいんだけど、5,6の実例がいきなり難しくなるという。MCMCとかPPKがどういった場面で使われるかとかそういうことが知りたい場合には役立つが、実際どうやって使うかとかは他の本のほうがよいかな。

• Kullback-Leibler情報量の解釈
• AICはその値に意味があるのではなく比較するモデルのAICの差に意味がある
• ベイズの定理を利用して推定されるものは薬物動態パラメータの事後分布

娘がブルーベリー大好きなのでちゃの生に狩りにいってきた。

なかなか細い路を縫っていく。そして茶畑。

取っても取ってもなくならないブルーベリーに娘は満足。

帰りにきわだ路で蕎麦。

utf8の話が参考になった。

文字コード超研究
深沢 千尋
ラトルズ / ￥ 3,129 ()
在庫あり。

ついでにExtlibのUTF8のソースも読んで理解を深めた。

# #require "extlib";;
/opt/local/lib/ocaml/site-lib/extlib: added to search path
/opt/local/lib/ocaml/site-lib/extlib/extLib.cma: loaded
# open UTF8;;
# let moji2 = "\xc3\x86";;
val moji2 : string = "\195\134"
# print_string moji2;; 
Æ- : unit = ()