20082009 q-chem
biphenylの立体構造はお互いのオルト位の水素がぶつかるのでねじれているんだけど、まぁそれはSTO-3Gで計算してもねじれてる構造が出てきた。
じゃぁ、水素じゃなければいいのか？ってことで片方をpyrimidineにしてみたら奇麗に平面になった(STO-3G)
ついでにHOMO,LUMOくらいも見てみた。
HOMO
LUMO
オチなし。
18082009 chemoinformatics bioinformatics q-chem
本が出てた
ドッキングシミュレーション関係の本だろうか。
タンパク質計算科学 ―基礎と創薬への応用― [CD-ROM付]あとGaussian
Gaussianプログラムによる量子化学計算マニュアル 計算入力法から実験値との比較までGaussianは使ってないのでこっちはあまり興味をそそられないが。
GAMESSでcation-πを計算してみる。
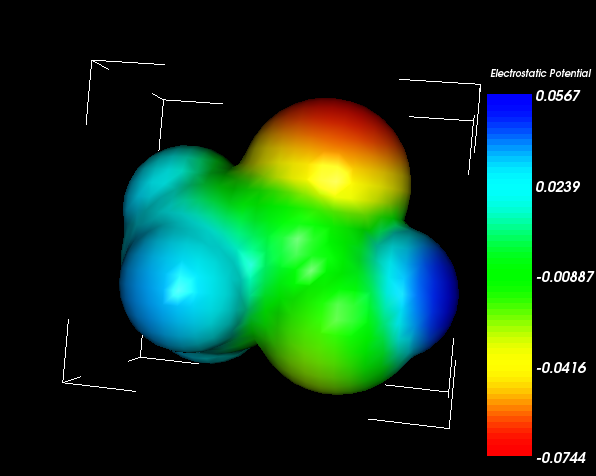
Cation-πってどのくらい安定化すんだろうか?と思っていたので計算してみる。
RCSBを適当にあさって見つけた、1R9LのBETとTRP188を切り出してモデル化する。
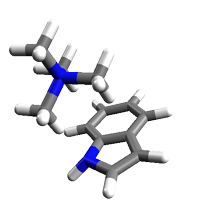
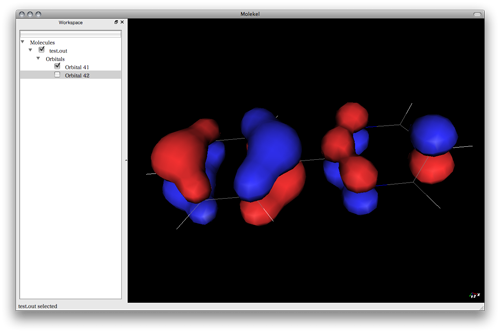
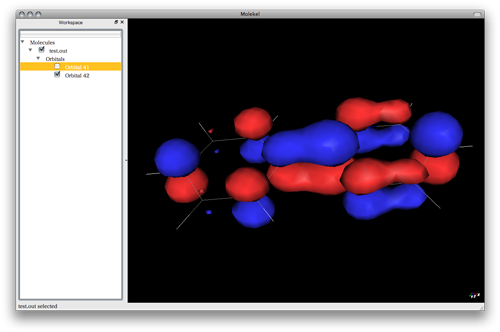
で、GAMESSで計算。
最初は6-31G+(d,p)で最適化しようと思ったのだけど、macbookだと全然終わらん。なのでSTO3Gでいいやと。TRPは無駄に計算量が増えるのだけどPHE,TYRあたりでモデル化できるのであればmacbookでも6-31G+(d,p)で計算できるような気がする。
------------------------------------
RESULTS OF KITAURA-MOROKUMA ANALYSIS
------------------------------------
HARTREE KCAL/MOLE
ELECTROSTATIC ENERGY ES= -0.011414 -7.16
EXCHANGE REPULSION ENERGY EX= 0.008788 5.51
POLARIZATION ENERGY PL= -0.001679 -1.05
CHARGE TRANSFER ENERGY CT= -0.007053 -4.43
HIGH ORDER COUPLING ENERGY MIX= 0.000166 0.10
TOTAL INTERACTION ENERGY, DELTA-E= -0.011193 -7.02
水素結合と同じくらいの強さかな。
以下、STO-3Gで構造最適化した座標を使ってつくったインプット
$BASIS GBASIS=STO NGAUSS=3 NDFUNC=1 $END
$CONTRL SCFTYP=RHF RUNTYP=MOROKUMA MAXIT=200 ICHARG=1 MULT=1 $END
$MOROKM IATM(1)=17 ICHM(1)=1 $END
$DATA
W188_BET.out
C1
N 7.0 26.56861 22.88472 72.47206
C 6.0 25.05591 23.05763 72.38527
C 6.0 27.18276 23.04159 71.08205
C 6.0 27.14794 23.94295 73.40648
C 6.0 26.89124 21.49601 73.01604
H 1.0 24.65761 22.29324 71.71973
H 1.0 24.84300 24.05067 71.99229
H 1.0 26.95089 24.04166 70.71972
H 1.0 26.73892 22.29197 70.42917
H 1.0 28.26387 22.89551 71.15590
H 1.0 26.89847 24.92550 73.00913
H 1.0 28.22884 23.81270 73.44995
H 1.0 26.70726 23.81001 74.39332
H 1.0 26.46855 20.75492 72.33939
H 1.0 26.44825 21.40230 74.00640
H 1.0 27.97398 21.38820 73.06968
H 1.0 24.63622 22.94695 73.38408
C 6.0 30.61324 20.49644 72.40614
C 6.0 30.47183 21.03406 71.19420
C 6.0 30.79531 21.59051 73.36029
C 6.0 30.75216 22.77934 72.62888
C 6.0 31.00908 21.63948 74.74382
N 7.0 30.43745 22.45766 71.27884
C 6.0 30.92671 24.02761 73.23103
C 6.0 31.18435 22.86580 75.34238
C 6.0 31.14962 24.05129 74.58925
H 1.0 30.33993 20.55500 70.23268
H 1.0 31.04481 20.72825 75.32842
H 1.0 30.86231 23.00634 70.52231
H 1.0 30.90815 24.93911 72.64846
H 1.0 31.36065 22.92555 76.40870
H 1.0 31.30378 24.99933 75.08996
H 1.0 30.61446 19.44515 72.64676
$END
すぐできる 量子化学計算ビギナーズマニュアル (KS化学専門書)26062009 q-chem
The Fragment Molecular Orbital Method
こんなの出てるのか
The Fragment Molecular Orbital Method: Practical Applications to Large Mokecular SystemsCrc Pr I Llc / ￥ 12,324 ()
通常9～13日以内に発送
買わねば
あと、インプットはここにあったので、論文読みながら実行すると吉。
25062009 q-chem
「基礎量子化学—軌道概念で化学を考える」を読んだ
良書だと思う。多少量子化学の知識は必要だけど。
分子軌道法（ＭＯ法）とは，原子に対する原子軌道の考え方を分子に対して適用し，分子の電子状態や反応機構を理解しようとするものである．この量子化学的視点を用いることによって，あらゆる化学現象を統一的に捉えて説明する．化学を学ぶもの必携の一冊．
基礎量子化学―軌道概念で化学を考える複合体結晶構造とかの結合の要因を探る時には、どうしても有機化学とか量子化学の知識が必要になってくる。且つドッキングというのは化学反応の特殊な一形態であり、それゆえ、弱い力に関する理論的な理解が必須となる（であろうと考えている）。
結局ドッキングというのは、反応により生成物が変わらない化学反応と捉えることができる。(結合を形成するようなものは自殺基質とか呼んで特殊な扱いをするね)
まぁそう考えれば、量子化学的な化学反応に対する理解は重要だろうと自然に導かれるけど。
- 第７章 分子構造の支配因子
- 第８章 分子間相互作用
- 第９章 分子構造と立体化学
- 第10章 官能基の性質と酸・塩基の強度
あたりは、コンフォメーションとか掘っていく際に役に立つはず。ただ、弱い相互作用に関する話は水素結合くらいしかなかったけど、結構詳しく載っていたので役立った。
その先のもっと弱い結合をどう評価していくかがテーマなんだけど、やっぱいまのところは論文を地道に追いかけていくしかないかな。
有機化学のための分子間力入門これも良い本なんだけど実例が基礎っぽすぎて、プラクティカルさが少し足りない。
24062009 q-chem
Energy Decomposition Analysis
複合体結晶構造から重要な残基とのインタラクションを見積もるのに、リガンドと特定の残基のシンプルなモデルを切り出してきて、きちんと計算すればよかろうと。
とか書いておいて、FMOの結果から相互作用の強いアミノ酸残基とリガンドを切り出してきて、morokuma-analysisしてみたけど、ちっとも収束しなかった。
うーん、これは困ったと、切り出したモデルでオプティマイズかけて再度計算してみたけどやっぱり収束しなかった。
結晶構造の座標みたいにあまり安定でないデータからエナジー出して、その成分をELECTROSTATIC,EXCHANGE REPULSION,POLARIZATION,CHARGE TRANSFERに分解する技術はきちんと押さえておく必要があるんだけど、どうやればいいんだろうか？
やっぱPIEDAの論文読んでおく必要ある？
43 Pair interaction energy decomposition analysis, D. G. Fedorov, K. Kitaura, J. Comp. Chem. 28 (2007) 222-237.
GAMESSでMOROKUMA ANALYSIS
MOROKUMA ANALYSISのサンプル(EXAM28)を。
水とアンモニアのダイマー計算
$contrl scftyp=rhf runtyp=morokuma coord=zmt $end
$basis gbasis=n31 ngauss=4 $end
$guess guess=huckel $end
$morokm iatm(1)=3 $end
$data
water-ammonia dimer
Cs
H
O 1 rOH
H 2 rOH 1 aHOH
N 2 R 1 aHOH 3 0.0
H 4 rNH 3 aHNaxis 1 180.0
H 4 rNH 3 aHNaxis 5 +120.0
H 4 rNH 3 aHNaxis 5 -120.0
rOH=0.956
aHOH=105.2
rNH=1.0124
aHNaxis=112.1451 ! makes HNH=106.67
R=2.93
$end
結果
HARTREE KCAL/MOLE
ELECTROSTATIC ENERGY ES= -0.022336 -14.02
EXCHANGE REPULSION ENERGY EX= 0.014308 8.98
POLARIZATION ENERGY PL= -0.001786 -1.12
CHARGE TRANSFER ENERGY CT= -0.003780 -2.37
HIGH ORDER COUPLING ENERGY MIX= -0.000687 -0.43
TOTAL INTERACTION ENERGY, DELTA-E= -0.014282 -8.96
DECOMPOSITION OF CT
CHARGE TRANSFER ENERGY, MON= 1 CT= -0.000494 -0.31
CHARGE TRANSFER ENERGY, MON= 2 CT= -0.003286 -2.06
DECOMPOSITION OF PL
EPL, MON= 1 PL= -0.001068 -0.67
EPL, MON= 2 PL= -0.000584 -0.37
HIGH ORDER COUPLING FOR PL, PMIX= -0.000133 -0.08
複合体結晶構造から重要な残基とのインタラクションを見積もるのに、リガンドと特定の 残基のシンプルなモデルを切り出してきて、きちんと計算すればよかろうと。
