26082009 Python
whichみたいなの、というか、外部プログラムを起動したいときに/usr/local/binにあるのか/opt/local/binにあったりするのだけどいちいち意識しなくていいようにスクリプト中で探したい。
例えばgaston
>>> filter(lambda f: os.path.isfile(f),[os.path.join(d,'gaston') for d in os.environ['PATH'].split(':')])
['/opt/local/bin/gaston', '/opt/local/bin/gaston']
最初にヒットしたものだけ
>>> filter(lambda f: os.path.isfile(f),[os.path.join(d,'gaston') for d in os.environ['PATH'].split(':')])[0]
'/opt/local/bin/gaston'
もっとうまいやりかたあるんだと思うんだけどわからんかった。
15082009 Python matplotlib PRML
PRML11章。一様乱数から正規乱数を発生させる。
from math import sin,cos,pi,log,sqrt
from random import random
def box_muller():
z1 = random()
z2 = random()
return sqrt(-2*log(z2)) * sin(2*pi*z1)
if __name__ == "__main__":
from pylab import *
x = [box_muller() for i in range(10000)]
hist(x,20)
savefig("box_muller.png")
最近、Journal of Pharmaceutical SciencesみたいなDMPKな雑誌を読むようになってきた。その中でScipyとpymcっていうpythonでMCMCができるモジュールを使って解析してた論文を見たので試したくなった。
パターン認識と機械学習 下 - ベイズ理論による統計的予測sudo easy_install-2.6 pymc
でさくっと入って、テストしてみたらなんか色々こけてるようなのだけど、とりあえずサンプル写経
import pymc
import numpy as np
n = 5*np.ones(4,dtype=int)
x = np.array([-.86,-.3,-.05,.73])
alpha = pymc.Normal('alpha',mu=0,tau=.01)
beta = pymc.Normal('beta',mu=0,tau=.01)
@pymc.deterministic
def theta(a=alpha, b=beta):
"""theta = logit^{-1}(a+b)"""
return pymc.invlogit(a+b*x)
d = pymc.Binomial('d', n=n, p=theta,value=np.array([0.,1.,3.,5.]),observed=True)
これをmymodel.pyって名前で保存しておいて
対話環境から
>>> import mymodel
>>> import pymc
>>> S = pymc.MCMC(mymodel, db='pickle')
>>> S.sample(iter=10000, burn=5000, thin=2)
>>> pymc.Matplot.plot(S)
>>> pymc.Matplot.savefig("test.png")
うーんMCMCわからん。精進せねば。
11072009 Python macbook matplotlib
macbookでmatplotlibを使っていたら出たエラー。
パターン認識と機械学習 上 - ベイズ理論による統計的予測LookupError: unknown encoding: X-MAC-JAPANESE
/opt/local/Library/Frameworks/Python.framework/Versions/2.6/lib/python2.6/site-packages/matplotlib/cbook.pyというファイルを書き換えた
def unicode_safe(s):
if preferredencoding is None: return unicode(s)
elif preferredencoding == 'X-MAC-JAPANESE': return unicode(s)
else: return unicode(s, preferredencoding)
04072009 Python
集合知プログラミングの著者が新しい本を出すみたい。
コードはpythonなのかな。 ちょっと気になる。
02072009 Python matplotlib
ローレンツのついでにgumowski
Programming the Semantic Webclass Gumowski:
"Gumowski-Mira Map"
def __init__(self, x0, y0, a):
self.x0 = x0; self.y0 = y0
self.a = a;
def f(self,x):
return self.a*x + 2*(1-self.a)*x**2/(1+x**2)
def calc(self, n):
dat = []
x,y = self.x0, self.y0
for i in range(n):
nx = y + self.f(x)
ny = -x + self.f(nx)
dat.append([nx,ny])
x,y = nx,ny
return dat
if __name__ == "__main__":
from pylab import *
from random import random
n = 3
for i in range(n*n):
p = str(n) + str(n) + str(i+1)
subplot(p)
a = random() * 0.1 + 0.3
gumow = Gumowski(20, 20, a)
dat = gumow.calc(1000)
x = [d[0] for d in dat]
y = [d[1] for d in dat]
plot(x,y,'bo', alpha=0.1,ms=5)
savefig("gumow.png")
01072009 Python matplotlib
どう書くより。
python+matplotlibで。
class Lorenz:
"Lorenz attractor"
def __init__(self, x0, y0, z0, p, r, b, dt):
self.x0 = x0; self.y0 = y0; self.z0 = z0
self.p = p; self.r = r; self.b = b
self.dt = dt
def calc(self, n):
dat = []
x,y,z = self.x0, self.y0, self.z0
for i in range(n):
dx = (-1 * self.p * x + self.p * y) * self.dt
dy = (-x * z + self.r * x - y) * self.dt
dz = (x * y - self.b * z) * self.dt
x += dx; y += dy; z += dz
dat.append([x,y,z])
return dat
if __name__ == "__main__":
from pylab import *
lorenz = Lorenz(1.0, 1.0, 1.0, 10.0, 28.0, 8.0/3.0, 0.01)
dat = lorenz.calc(5000)
x = [d[0] for d in dat]
y = [d[1] for d in dat]
plot(x,y)
savefig("lorenz.png")
演習本にデコンボリューション法が載っていたのだけど、実装までは載ってなかったので、調べたら、論文が見つかった。
GOTOとIFの組み合わせがwhileなのかforなのか悩むとこが幾つかあったが、pythonで書きなおした。結構、fortranっぽさが残っている気もするが。
ファーマコキネティクス―演習による理解#!/usr/bin/env python
def calc_eps():
eps = 1.0
while eps + 1.0 > 1.0: eps = eps/2.0
return eps
def sign(a1,a2):
if a2 >= 0: return abs(a1)
else: return -abs(a1)
def deconv(a,div,b,dose):
n = len(a); m = len(b); l = n + m -1
eps = calc_eps()
u = [0.0 for i in range(l)]
v = [0.0 for i in range(l)]
gamma = [0.0 for i in range(20)]
g = [0.0 for i in range(20)]
a.sort(lambda x,y:cmp(x[1],y[1]))
for II in range(n-1):
x1 = a[II][1] * -1
x2 = a[II+1][1] * -1
qx1 = 0.0
qx2 = 0.0
for i in range(n):
s1 = 1.0
s2 = 1.0
for j in range(n):
if j != i:
s1 = s1*(a[j][1] + x1)
s2 = s2*(a[j][1] + x2)
qx1 = qx1 + a[i][0] * s1
qx2 = qx2 + a[i][0] * s2
x3 = x1
qx3 = qx1
d = x2 -x1
e = d
while(1):
if abs(qx3) < abs(qx2):
x1 = x2; x2 = x3; x3 = x1
qx1 = qx2; qx2 = qx3; qx3 = qx1
tol = 4.0*eps*abs(x2)
xm = 0.5*(x3-x2)
if abs(xm) <= tol or qx2 == 0.0: break
if abs(e) >= tol and abs(qx1) > abs(qx2):
if x1 == x3:
s = qx2/qx1; p = 2.0*xm*s; q = 1.0-s
else:
q = qx1/qx3; r = qx2/qx3; s = qx2/qx1
p = s*(2.0*xm*q*(q-r) - (x2-x1)*(r-1.0))
q = (q-1.0)*(r-1.0)*(s-1.0)
if p > 0.0: q = -q
p = abs(p)
if 2.0*p < 3.0*xm*q - abs(tol*q) and p < abs(0.5*e*q):
e = d
d = p/q
else:
d = xm
e = d
else:
d = xm
e = d
x1 = x2
qx1 =qx2
x2 = x2 + d
if abs(d) <= tol: x2 = x2 - d + sign(tol,xm)
qx2 = 0.0
for i in range(n):
s2 = 1.0
for j in range(n):
if j != i: s2 = s2*(a[j][1] +x2)
qx2 = qx2 + a[i][0] * s2
if qx2*(qx3/abs(qx3)) > 0.0:
x3 = x1
qx3 = qx1
d = x2 - x1
e = d
gamma[II] = x2
s2 = 0.0
for j in range(n):
s1 = 0.0
for k in range(n):
if k != j:
s1 = s1 + 1.0/(gamma[II] + a[k][1])
s2 = s2 + a[j][0]*s1/(gamma[II] + a[j][1])
g[II] = 1.0/s2
ak1 = 0.0
ak2 = 0.0
ak3 = 0.0
for i in range(n):
ak1 = ak1 + a[i][0];
ak2 = ak2 + a[i][0]*a[i][1]
if n > 1 and i != n-1: ak3 = ak3 + g[i]/gamma[i]
ak1 = 1.0/ak1
ak2 = ak1*ak1*ak2
ak3 = ak2 - ak3
ak4 = 100.0*div/dose
uz = 0.0
for i in range(l):
s = 0.0
if i > m-1:
v[i] = -gamma[i-m]
for j in range(m):
s = s + b[j][0]/(gamma[i-m] + b[j][1])
u[i] = ak4*g[i-m]*s/gamma[i-m]
else:
v[i] = b[i][1]
u[i] = ak4*b[i][0]*(ak1 - ak3/b[i][1])
if n != 1:
for j in range(n-1):
s = s + g[j]/(gamma[j]*(gamma[j] + b[i][1]))
u[i] = u[i] - ak4*b[i][0]*s
uz = uz - u[i]
return uz,u,v
if __name__ =='__main__':
print "=== Data set 1 ==="
a = [[1.0427,5.0526],[0.97617,0.97567]]
div = 1.0
b = [[-0.80547,3.6373],[0.80547,0.83033]]
dose = 0.6
print deconv(a,div,b,dose)
print "=== Data set 2 ==="
a = [[1.3377,3.1851],[0.52381,0.61065]]
div = 1.0
b = [[-2.2637,2.0800],[2.2637,1.2513]]
dose = 0.6
print deconv(a,div,b,dose)
print "=== Data set 3 ==="
a = [[1.0308,5.9131],[1.0487,1.0262]]
div = 1.0
b = [[-1.6103,3.3563],[1.6103,1.3917]]
dose = 0.6
print deconv(a,div,b,dose)
print "=== Data set 4 ==="
a = [[1.3377,3.1851],[0.52381,0.61065]]
div = 1.0
b = [[-5.5440,2.2488],[5.5440,1.7521]]
dose = 0.6
print deconv(a,div,b,dose)
Table.1 のテスト計算を実行。論文のデータセット4のa2はタイポでしょう。
=== Data set 1 ===
(103.38116460095375,
[99.756988719460651, -23.218031509886707, -179.92012181052769],
[3.6373000000000002, 0.83033000000000001, 2.9469592648362699])
=== Data set 2 ===
(94.012343334076377,
[212.39909284817011, 2395.320119577972, -2701.7315557602187],
[2.0800000000000001, 1.2513000000000001, 1.3350740721242431])
=== Data set 3 ===
(94.362883301636657,
[-1704.7606134762168, 73.013373899587776, 1537.3843562749923],
[3.3563000000000001, 1.3916999999999999, 3.4906828227939406])
=== Data set 4 ===
(91.15932635164495,
[370.51731307178676, -1111.1884882257646, 649.51184880233291],
[2.2488000000000001, 1.7521, 1.3350740721242431])
21062009 Python
整数で割る際にfloatの数値が欲しいときに2.0と書いてたけど0は必要ないらしい
>>> 1/2
0
>>> 1/2.
0.5
>>> 1./2
0.5
でもちょっと読みにくいので、今まで通りきちんと書くかな。
16062009 Python
グラフつくるとことは禁断探索法と一緒。
メタヒューリスティクスの数理def evaluate(nodes, adj, sol, alpha):
s = [0 for i in nodes]
d = [0 for i in nodes]
bal = 0
for i in nodes:
if sol[i] == 0:
bal += 1
else:
bal -= 1
for j in adj[i]:
if sol[j] == sol[i]:
s[i] += 1
else:
s[i] -= 1
cost = 0
for i in nodes: cost += d[i]
cost /= 2
cost += alpha*abs(bal)
return cost, bal, s, d
def find_move_rnd(n, sol, alpha, s, d, bal):
istar = random.randint(0,n-1)
part = sol[istar]
if part == 0 and bal > 0 or part == 1 and bal < 0:
penalty = -2*alpha
else:
penalty = 2*alpha
delta = s[istar] - d[istar] + penalty
return istar, delta
def update_move(adj, sol, s, d, bal, istar):
part = sol[istar]
sol[istar] = 1-part
s[istar], d[istar] = d[istar], s[istar]
for j in adj[istar]:
if sol[j] == part:
s[j] -= 1
d[j] += 1
else:
s[j] += 1
d[j] -= 1
if part == 0:
bal -= 1
else:
bal += 1
return bal
def estimate_temperature(n, sol, s, d, bal, initprob):
ntrials = 10 * len(sol)
nsucc = 0
deltaZ = 0.0
for i in range(0,ntrials):
part = random.randint(0,1)
istar, delta = find_move_rnd(n, sol, alpha, s, d, bal)
if delta > 0:
nsucc += 1
deltaZ += delta
if nsucc != 0:
deltaZ /= nsucc
T = -deltaZ/math.log(initprob)
return T
def metropolis(T, delta):
if delta <= 0 or random.random() < math.exp(-(delta)/T):
return True
else:
return False
def annealing(nodes, adj, sol, initprob, tempfactor, sizefactor, cutoff, freezelim, minpercent, alpha):
n = len(nodes)
z,bal,s,d = evaluate(nodes, adj, sol, alpha)
if bal == 0:
solstar, zstar = list(sol), z
T = estimate_temperature(n, sol, s, d, bal, initprob)
nfrozen = 0
part = 0
while nfrozen < freezelim:
changes, trials = 0,0
while trials < n*sizefactor and changes < n*cutoff:
trials += 1
istar, delta = find_move_rnd(n, sol, alpha, s, d, bal)
if metropolis(T, delta):
changes += 1
bal = update_move(adj, sol, s, d, bal, istar)
z += delta
if bal == 0:
if z < zstar and part == 0:
solstar, zstar = list(sol), z
nfrozen = 0
T *= tempfactor
if float(changes)/trials < minpercent:
nfrozen += 1
return solstar, zstar
if __name__ == "__main__":
import networkx as nx
import matplotlib.pyplot as plt
num_nodes = 50
nodes, adj = rnd_graph_fast(num_nodes,0.3)
G=nx.Graph()
for i in range(num_nodes):
G.add_node(i)
for i in range(num_nodes-1):
for j in adj[i]:
if i < j:
G.add_edge(i,j)
pos=nx.spring_layout(G)
initprob = .4 # initial acceptance probability
sizefactor = 16 # for det. # tentatives at each temp.
tempfactor = .95 # cooling ratio
freezelim = 5 # max number of iterations with less that minpercent acceptances
minpercent = .02 # fraction of accepted moves for being not frozen
alpha = .05 # imballance factor
N = len(nodes) # neighborhood size
L = N*sizefactor # number of tentatives at current temperature
sol = construct(nodes)
z,bal,s,d = evaluate(nodes, adj, sol, alpha)
sol,z = annealing(nodes, adj, sol, initprob, tempfactor, N, L, freezelim, minpercent, alpha)
zp,bal,sp,dp = evaluate(nodes, adj, sol, alpha)
rnodelist = []
bnodelist = []
for i in range(len(sol)):
if sol[i] == 1:
rnodelist.append(i)
else:
bnodelist.append(i)
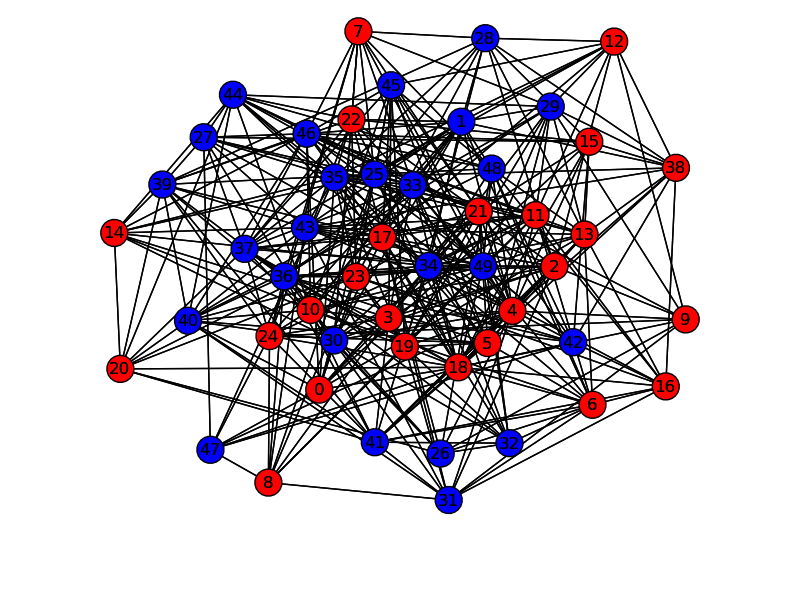
nx.draw(G,pos,nodelist=rnodelist,node_color='r')
nx.draw(G,pos,nodelist=bnodelist,node_color='b')
plt.savefig("path.png")
