15042010 PRML
4.2にちょっと感動。
ロジスティック回帰で出てくるオッズ比はまぁそんなもんなのかなとかいって天下り的に覚えてたんだけど。
クラス分類の事後確率から考えていくほうが僕にとっては自然だ。
2クラスの分類問題（活性ありなしとか）を考えると事後確率は以下の式で表される。
分子で割ると
但し、αは以下の式で表される。
これはロジスティックシグモイド関数となる。
パターン認識と機械学習 上 - ベイズ理論による統計的予測14042010 PRML
パーセプトロン
パターン認識と機械学習を読み直していて今4章。
図4.7のパーセプトロンのイメージが大変わかりやすいことに気づいて感激したのであった。
いまは、Pinheiroを読むのに苦労している。
Mixed-Effects Models in S and S-PLUS (Statistics and Computing)José Pinheiro
Springer / 2859円 ( 2009-04-15 )
これをきちんと理解しないと、PK-PDが進まないんだよな。
Pharmacokinetic-Pharmacodynamic Modeling And SimulationPeter L., Ph.D. Bonate
Springer / 7596円 ( 2005-11 )
JAGSでマルコフ連鎖モンテカルロ法
連休は旅行いったりとか子供と遊んでたんだけどそれ以外はJAGSいじってた。
マルコフ連鎖モンテカルロ法 (統計ライブラリー)5章をWikiに書いていくことにした。
分散分析のあたりを出来るようにしておくとよいと思った。
- 5.1 ロジスティック回帰モデル
- 5.2 メタ分析
- 5.3 多項ロジットモデル
- 5.4 対数線形モデル
- 5.5 ポアソン回帰
- 5.6 2値データに対する回帰分析
- 5.7 トービット回帰モデル
- 5.8 変曲点のある回帰分析
- 5.9 生存時間分析(ワイブル回帰)
- 5.10 生存時間分析(コックス回帰)
- 5.11 時系列モデル
- 5.12 分散分析
- 5.13 分散成分分析
- 5.14 分散分析(枝分かれ配置)
- 5.15 一般化可能性理論
- 5.16 反復測定データの分散分析
- 5.17 階層線形モデル
- 5.18 項目反応理論(2母数2値モデル)
- 5.19 項目反応理論(段階反応モデル)
- 5.20 項目反応理論(名義反応モデル)
- 5.21 項目反応理論(部分採点・評定尺度モデル)
- 5.22 項目反応理論(連続反応モデル)
- 5.23 多次元IRT
- 5.24 項目反応理論(混合名義反応モデル)
- 5.25 項目反応理論における特異項目機能(DIF) の分析
- 5.26 正規混合モデル
- 5.27 潜在クラス分析
- 5.28 成長曲線モデル
- 5.29 非線形成長曲線モデル
- 5.30 因子分析
- 5.31 多母集団分析
- 5.32 非線形SEM
あとこの本だけだと難しすぎるのでPRMLの下巻が必須(多分)。
パターン認識と機械学習 下 - ベイズ理論による統計的予測SIR(sampling-importance-resampling)
水産資源学におけるベイズ統計の応用ワークショップのスライドの22,23枚目
- g(x)からM個のサンプルx1*, …, xM*を発生
- w*= f(x*)/g(x*)を計算
- x1*, …, xM*からw1*, …, wM*に比例する確率でサンプルをm個とってくる
- 得られたm個のサンプルはf(x)からの事後サンプル
となっているのだが、23枚目のRのコードは
n2 <-sample(length(x1), 1000, replace=T, prob=dlnorm(x1,1.1,0.6))
とwを求めずにいきなりサンプリングしているので？となったが、一様分布だから重みを計算する必要ないのね。
わざわざ書くならこうか。
x1 <-runif(100000,0,60)
w <- dlnorm(x1,1.1,0.6) / (dunif(x1,0,60))
n2 <-sample(length(x1), 1000, replace=T, prob=w)
x2 <-x1[n2]
plot(density(x2))
15082009 Python matplotlib PRML
Box-MullerをPythonで
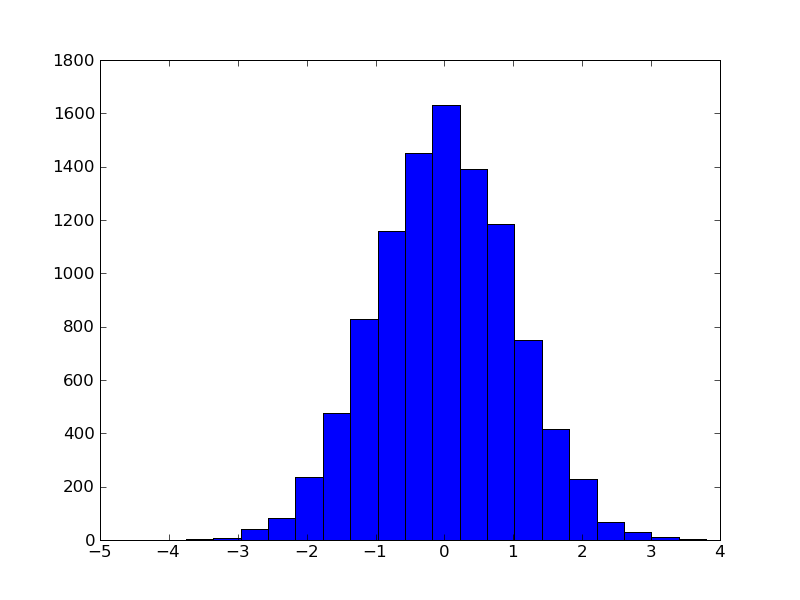
PRML11章。一様乱数から正規乱数を発生させる。
from math import sin,cos,pi,log,sqrt
from random import random
def box_muller():
z1 = random()
z2 = random()
return sqrt(-2*log(z2)) * sin(2*pi*z1)
if __name__ == "__main__":
from pylab import *
x = [box_muller() for i in range(10000)]
hist(x,20)
savefig("box_muller.png")
13082009 chemoinformatics R PRML
Rでベータ分布
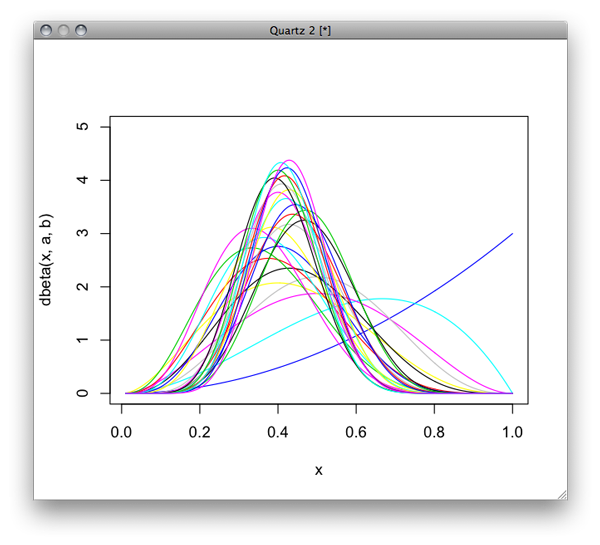
PRMLも再読してるが、手動かしながら読むほうがしっくりくる。 p.70のベータ分布の逐次学習ってのが面白そうなのでやってみた。
data <- rbinom(30,1,0.5)
plot_dbeta <- function(data){
a <- 0
b <- 0
x <- seq(0.01, 1.0, len = 500)
for (i in 1:length(data)) {
if(data[i] == 1) { a = a + 1 }
else { b = b + 1 }
if(i>3){
if(i==4){ plot(x, dbeta(x,a,b),type = "l",col=i,ylim=c(0,5)) }
else { plot(x, dbeta(x,a,b),type = "l",col=i,xlab="",ylab="",axes=F,ylim=c(0,5)) }
par(new=T)
}
}
}
二項分布で30個のリストを発生させて読みながらa,bのデータを更新していきつつその時のベータ分布の密度を求めつつプロットしていくという操作。
> data
[1] 1 0 1 1 0 0 0 1 0 0 0 1 0 0 1 1 1 0 1 0 0 0 1 0 0 1 0 1 0
[30] 1
データはこんな感じで、4番目のデータからプロットしていくとだんだん二項分布に近づいていく様がみてとれる。
15112008 chemoinformatics bioinformatics PRML
Dirichlet Process
chemoinformaticsにも使えそうなので色々読んでみている。
- Gaussian processes define a distribution over functions
- Dirichlet processes define a distribution over distributions
ぼんやりとした入門のそのまた入門の入り口ぐらいには立ったかなって感じ。CRPで遺伝子発現のクラスタリングをやっている論文があったので読む。
- Dirichlet Processes: Tutorial and Practical Course
- mots quotidiens.
- Ghahramani の UAI'05のスライド
- Dirichlet Process を用いた クラスタリング
- Clustering microarray gene expression data using weighted Chinese restaurant process
- Automated Discovery of Functional Generality of Human Gene Expression Programs
ディリクレ分布に関してはこの本見た。
ICAからモデルベースのクラスタリング
昨日気になったので、とりあえずどんな感じか確かめようと。
> library("fastICA") > library("mclust") > data("iris") > b <- fastICA(iris[1:4],2) > mc <- Mclust(b$S,G=3,modelNames="VVV") > plot(mc,b$S)
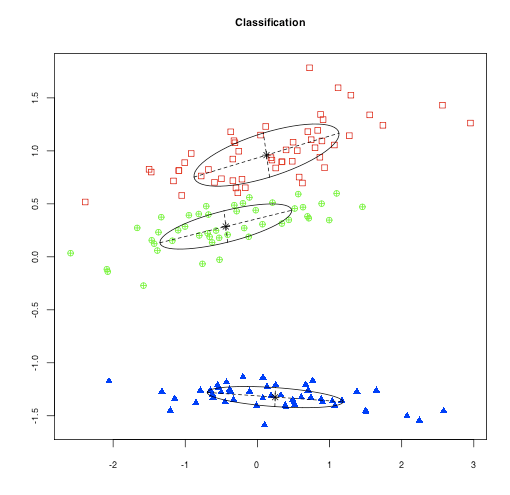
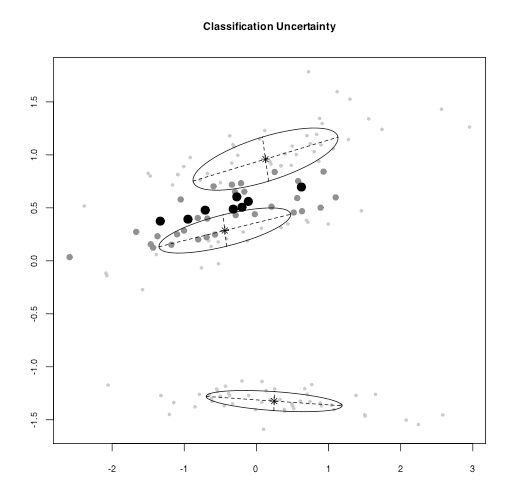
混合分布はクラスタリングの本にも載っているが、PRMLの下巻のほうがK-meansからEM,混合モデルの導入の流れがスムーズで分かりやすかったかな。
Rで学ぶクラスタ解析