X-meansの論文を眺めていたら、最初から2-meansやってBICが大きくなる限り再帰的に2-meansやればいいんじゃないの?と思ったので、そういう風なものを書いてみたという。
- 最初のデータのBICをもとめます
- 2-meansでクラス分割してみて、分割後のBICのほうが高い場合分割します。BICが低くなる場合にはそれ以上わけられないので、それ以上分割はしません。
- 分割出来た場合はそれぞれのクラスをさらに分割できるか試してみます。
K-meansのコードは「集合知プログラミング」のものを参考にした。データも集合知プログラミングのブログのデータを使ってます
 集合知プログラミング
集合知プログラミング
Toby Segaran
オライリージャパン / ¥ 3,570 ()
在庫あり。
コードは分散のとことか、結局クラスのデータが一つ二つになっちゃった場合とかのエラーに対応すんのがめんどくなって適当にいじってるのでかなりいい加減というかいい加減すぎなのでダメすぎなので、そういうかんじで。BICもきちんと理解しないといけないのだけど、とりあえずやっつけ的になってしまった。
import random
from math import sqrt,pi,log
def pearson(v1,v2):
sum1=sum(v1)
sum2=sum(v2)
sum1Sq=sum([pow(v,2) for v in v1])
sum2Sq=sum([pow(v,2) for v in v2])
pSum=sum([v1[i]*v2[i] for i in range(len(v1))])
num=pSum-(sum1*sum2/len(v1))
den=sqrt((sum1Sq-pow(sum1,2)/len(v1))*(sum2Sq-pow(sum2,2)/len(v1)))
if den==0: return 0
return 1.0-num/den
def euclid(v1,v2) :
return sqrt(sum([pow(v1[i]-v2[i],2) for i in range(len(v1))]))
def kcluster(rows,cluster,distance=euclid,k=2):
ranges=[(min([rows[c][i] for c in cluster]),max([rows[c][i] for c in cluster]))
for i in range(len(rows[0]))]
clusters=[[random.random()*(ranges[i][1]-ranges[i][0])+ranges[i][0]
for i in range(len(rows[0]))] for j in range(k)]
lastmatches = None
for t in range(100):
bestmatches=[[] for i in range(k)]
for j in cluster:
row = rows[j]
bestmatch = 0
for i in range(k):
d = distance(clusters[i],row)
if d < distance(clusters[bestmatch],row): bestmatch=i
bestmatches[bestmatch].append(j)
if bestmatches == lastmatches: break
lastmatches = bestmatches
for i in range(k):
avgs=[0.0]*len(rows[0])
if len(bestmatches[i])>0:
for rowid in bestmatches[i]:
for m in range(len(rows[rowid])):
avgs[m]+=rows[rowid][m]
for j in range(len(avgs)):
avgs[j]/=len(bestmatches[i])
clusters[i]=avgs
return bestmatches,clusters
def readfile(filename):
lines=[line for line in file(filename)]
colnames=lines[0].strip().split('\t')[1:]
rownames=[]
data=[]
for line in lines[1:]:
p=line.strip().split('\t')
rownames.append(p[0])
data.append([float(x) for x in p[1:]])
return rownames,colnames,data
def likelihood(data,cluster,avg_cluster,k):
sample_number = len(cluster)
variance = sum([pow(data[c][i] - avg_cluster[i],2) for i in range(len(avg_cluster)) for c in cluster]) / float(sample_number)
if variance == 0: variance = 0.0000000000000001
lkh = -sample_number/2*log(2*pi) - sample_number*len(avg_cluster)/2*log(variance) - (sample_number - k)/2 + sample_number*log(sample_number)
return lkh
def _xcluster(data,cluster,bic,k):
bm,cl = kcluster(data,cluster)
if len(bm[0]) == 0 or len(bm[1]) == 0:
bm,cl = kcluster(data,cluster)
new_likelihood = likelihood(data,bm[0],cl[0],2) + likelihood(data,bm[1],cl[1],2)
new_bic = new_likelihood - (2*len(data[0])+1)/2 * log(len(cluster))
if bic < new_bic:
if len(bm[0]) > 1:
bicl = likelihood(data,bm[0],cl[0],1) - (len(data[0])+1)*log(len(bm[0]))/2
nl = _xcluster(data,bm[0],bicl,2)
else:
nl = bm[0]
if len(bm[1]) > 1:
bicr = likelihood(data,bm[1],cl[1],1) - (len(data[0])+1)*log(len(bm[1]))/2
nr = _xcluster(data,bm[1],bicr,2)
else:
nr = bm[1]
return [nl,nr]
else:
return cluster
def xcluster(filename,distance=euclid,k=2):
rownames,colnames,data = readfile(filename)
sample_number = len(data)
params = len(data[0])
avg = [sum([data[j][i] for j in range(sample_number)])/float(sample_number) for i in range(params)]
bic = likelihood(data,range(len(data)),avg,1) - (params+1)*log(sample_number)/2
bestclusters = _xcluster(data,range(sample_number),bic,2)
return bestclusters
コードはいろんな部分がダメすぎてあれなんだけど、とりあえず実行。
>>> from xmeans import *
>>> xcluster("blogdata.txt")
[[[[[[[0, 2, 3, 5, 7, 8, 11, 12, 13, 15, 16, 17, 20, 21, 22, 26, 28, 29,
30, 32, 34, 36, 38, 39, 40, 43, 47, 48, 50, 51, 52, 53, 54, 55, 56, 57, 58,
59, 60, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 74, 75, 76, 77, 78, 79, 80,
83, 84, 86, 87, 88, 89, 92, 95, 96, 97], [44]], [[91], [37]]], [1, 6, 9,
10, 14, 18, 19, 27, 31, 33, 35, 45, 61, 73, 82, 90, 93, 98]], [[85], [[23],
[[25], [[[49], [94]], [62]]]]]], [[4], [[81], [[42], [[41], [46]]]]]], [24]]
あとで、もうちょっと考える。
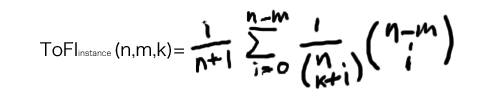

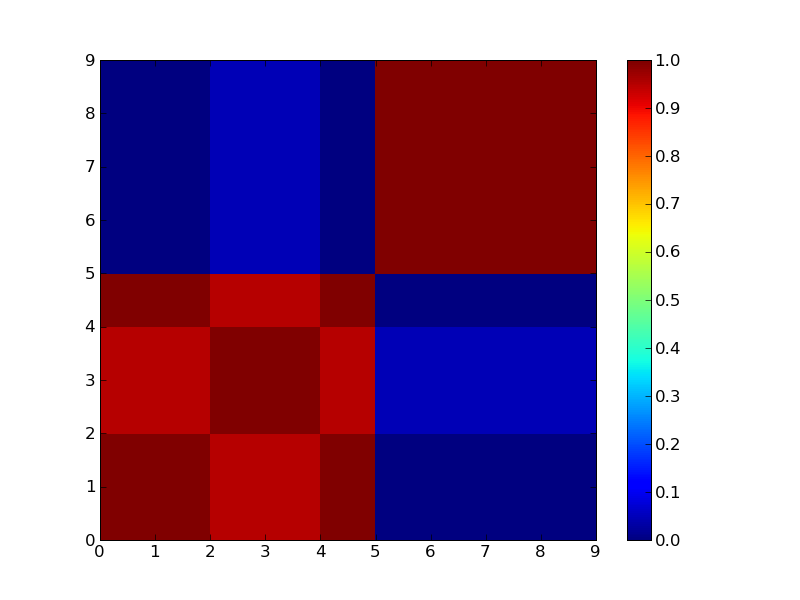
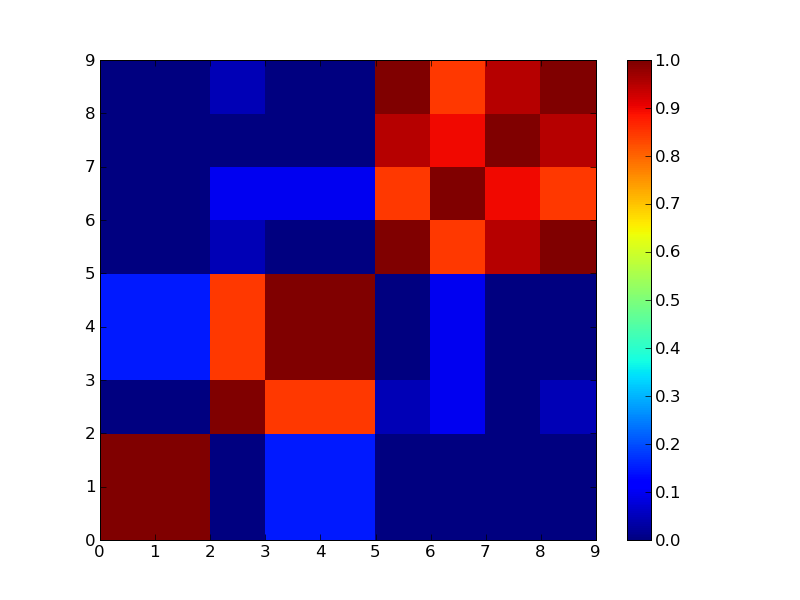
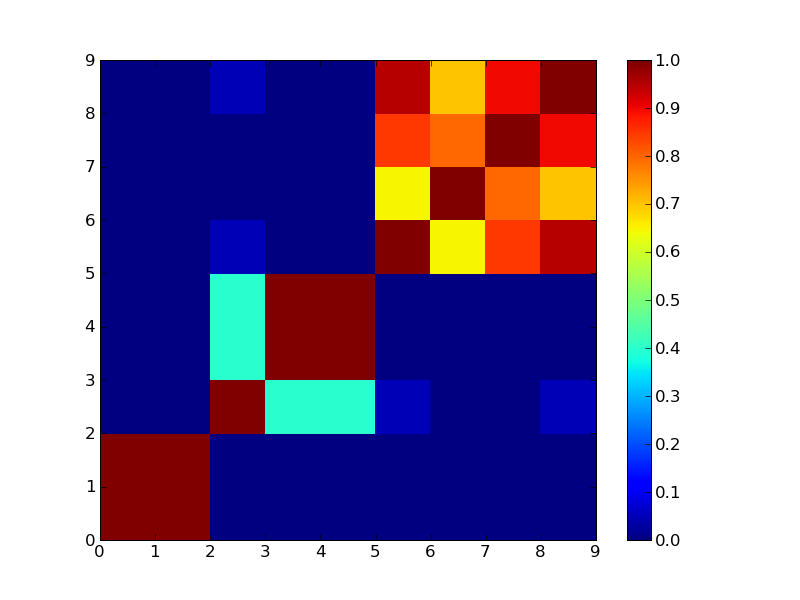
 集合知プログラミング
集合知プログラミング
 Beginning Python Visualization: Crafting Visual Transformation Scripts (Books for Professionals by Professionals)
Beginning Python Visualization: Crafting Visual Transformation Scripts (Books for Professionals by Professionals) ビジュアライジング・データ ―Processingによる情報視覚化手法
ビジュアライジング・データ ―Processingによる情報視覚化手法 バイオインフォマティクスのためのPerl入門
バイオインフォマティクスのためのPerl入門 実践 バイオインフォマティクス -ゲノム研究のためのコンピュータスキル-
実践 バイオインフォマティクス -ゲノム研究のためのコンピュータスキル-