12 01 2010 chemoinformatics bioinformatics Python Tweet
NMFを追っかけてたらMetagenes and molecular pattern discovery using matrix factorizationという論文を見つけたので、週末はこの論文を読みながら色々やってみた。NMFの便利なところは元の特徴(この論文の場合は遺伝子発現量)からより少ない任意の特徴量(論文中ではmetagene)に変換できるところであり、さらにそのままクラスターの分割に利用できる。
たとえば2つのmetageneで表現した場合、より発現量の大きいmetageneで分割すれば2つのクラスに分けられる。(QSARだったらdescriptorからmeta discriptorが導かれてそれに基づいてクラス分類ができるでしょう)
続いて、重要なのがクラスの安定性である。要するに最適なクラスタの数はいくつなのかということである。これに対して、この論文ではConsensus Clusteringというリサンプリングと隣接行列(connectivity matrix)を利用する方法をモディファイした方法を使っている。
ここで隣接行列はi番目のサンプルとj番目のサンプルが同じクラスなら1、それ以外なら0である。この行列のn回の平均値をコンセンサスマトリックスとする。コンセンサスマトリックスの値は0-1の間をとり、サンプルi,jが常に同じクラスになる場合は1、常に異なるクラスの場合は0である。フラフラするばあいはその間の値をとる。元の論文のconsensus clusteringアルゴリズムはデータの80%をランダムサンプリングして評価するのに対し、NMFの場合、初期値の行列はランダムな数字にしているので適当にループ(n)をまわすだけでよい。
NMFの実装は集合知プログラミングのものを用い、コンセンサスマトリックスを評価するコードをnumpyを使ってかいた。
import nmf
from numpy import *
def consensus(a,kstart,kend,nloop):
""" calculate consensus matrix
"""
(n,m) = a.shape
consensus = zeros((kend+1,m,m))
conn = zeros((m,m))
#i = 0
for j in range(kstart,kend+1):
connac = zeros((m,m))
for l in range(nloop):
#i += 1
(w,h) = nmf.factorize(a,pc=j)
conn = nmfconnectivity(h)
connac = connac + conn
consensus[j] = connac / float(nloop)
return consensus
def nmfconnectivity(h):
""" calculate connective matrix
"""
(k,m) = h.shape
ar = []
for i in range(m):
max_i = 0
max_v = 0
for index,v in enumerate(h[:,i]):
if v > max_v :
max_v = v
max_i = index
ar.append(max_i)
mat1 = tile(matrix(ar),(m,1))
mat2 = tile(matrix(ar).T,(1,m))
return array(mat1 == mat2, dtype=int)
これをcc.pyという名前で保存しテスト用のセットを適当に用意して実行。
from numpy import *
from pylab import *
import cc
kstart = 2
kend = 4
testarray = array([[0,0,1,1,1,0,0,0,0],
[0,0,1,1,0,0,0,0,0],
[1,1,0,0,1,1,0,0,1],
[1,1,0,0,0,0,0,1,0],
[1,1,0,1,0,0,0,0,0],
[0,0,0,0,0,1,1,1,1],
[1,0,0,0,0,1,1,1,0],
[0,0,0,0,0,0,1,1,1],
[0,0,0,1,0,1,1,1,1]
])
cons = cc.consensus(testarray.T,kstart,kend+1,20)
for i in range(kstart,kend+1):
pcolormesh(cons[i])
if i == kstart:
colorbar()
savefig('ccr' + str(i) + '.png')
見ればすぐ分かるが3つにクラスタリングできそうなマトリックス。
結果
2クラスタで分けた場合。
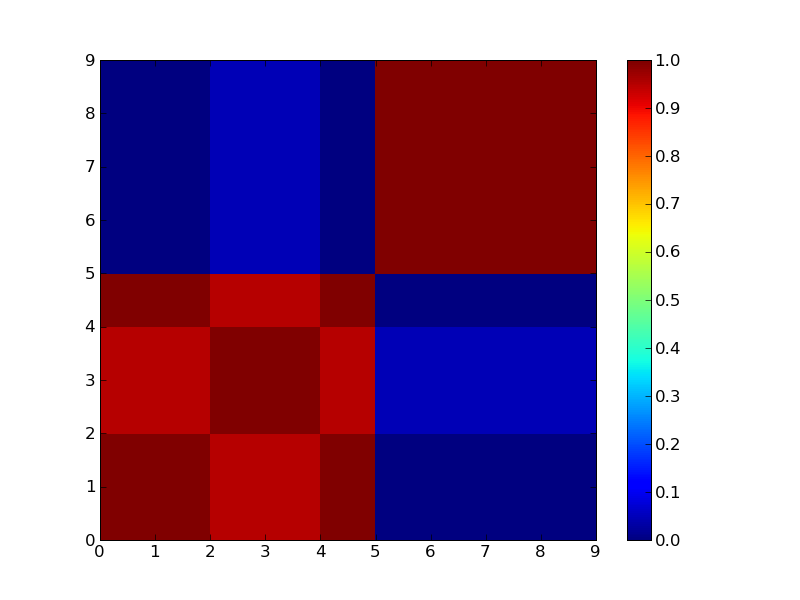
3クラスタで分けた場合
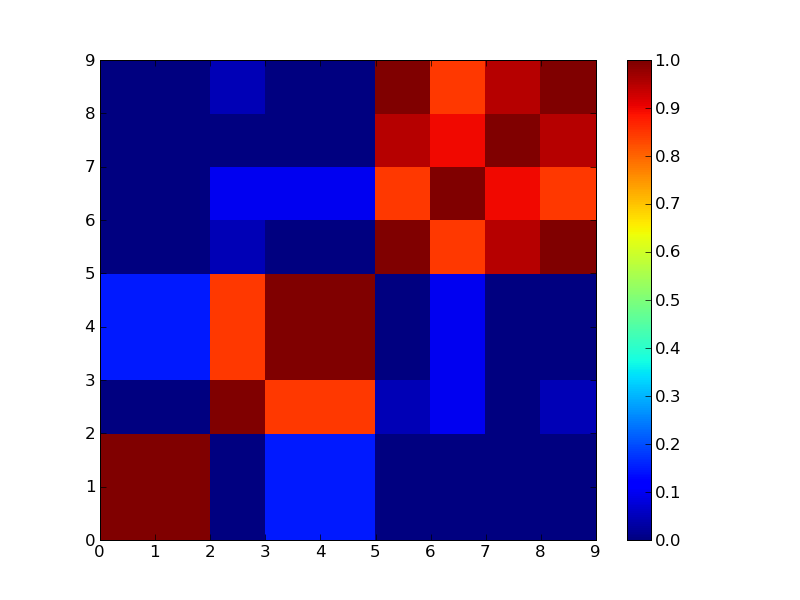
4クラスタで分けた場合
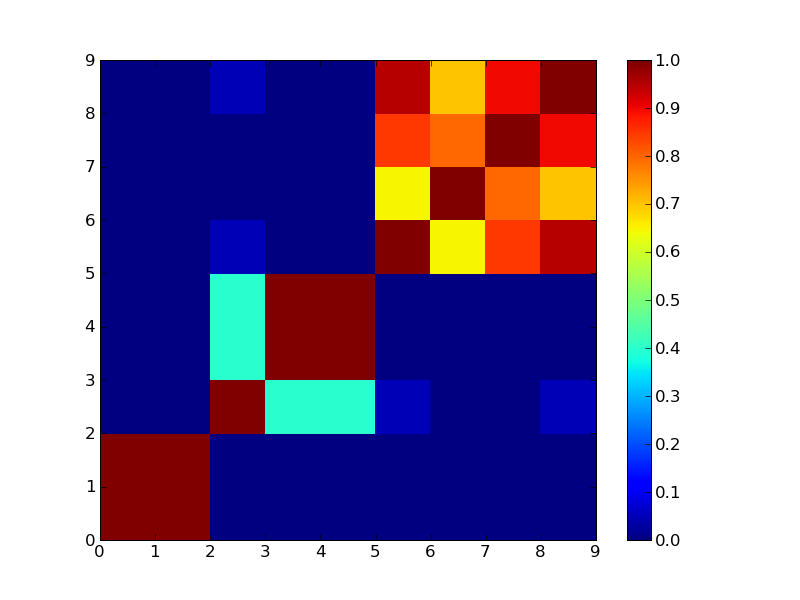
もうちょっと実際のデータでやってみないとあれだなぁ。それとConsensus ClusteringのCDFプロットみたいなのが欲しいところ。
参考書籍
参考論文

 集合知プログラミング
集合知プログラミング