Drkcore

06082009 R DMPK

PK8-4

Caco-2細胞のモデリング

ファーマコキネティクス―演習による理解
杉山雄一,山下伸二,加藤基浩
南山堂 / ￥ 6,300 ()
通常2～5週間以内に発送

設問1

Vmax は結合サイト数、ATPターンオーバー、細胞総数からもとまる

> 100000*1e+6*25/6.02e+23*60
[1] 2.491694e-10

つまり2.491694(nmol/min)

library(odesolve)
params = c(Vmax=2.491694*10^-3,S=4.71,Pa=5e-6,Pb=3e-6,Km=0.3,Va=1.5,Vc=0.025,Vb=3.0)
times=c(0,(1:60))

dydt <- function(t,y,p){
Vmax <- p['Vmax']
S <- p['S']
Pa <- p['Pa']
Pb <- p['Pb']
Km <- p['Km']
Va <- p['Va']
Vc <- p['Vc']
Vb <- p['Vb']
Ca <- (S*Pa*(y[2]-y[1]) + Vmax*y[2]/(Km+y[2]))/Va
Cc <- (S*(Pa*(y[1]-y[2]) + Pb*(y[3]-y[2])) - Vmax*y[2]/(Km+y[2]))/Vc
Cb <- (S*Pb*(y[2]-y[3]))/Vb
return(list(c(Ca,Cc,Cb)))
}

濃度リストをあたえるとPeffのリストを返す関数を書いておく。

calc <- function(dose_list){
l <- c()
for (dose in dose_list){
    y <- lsoda(c(Ca=dose,Cc=0.0,Cb=0.0),times,dydt,params)  
    Y <- data.frame(y)
    res <- lm(Cb ~ time,Y[c("time","Cb")][seq(41,61),])
    Peff <- res$coefficients[2]*3/(4.71*dose)
    l <- append(l,Peff)
}
return(l)
}

d <- c(0.1,0.3,0.6,1,3,6,10,30,60,100,300,600,900,1000)
peffs <- calc(d)
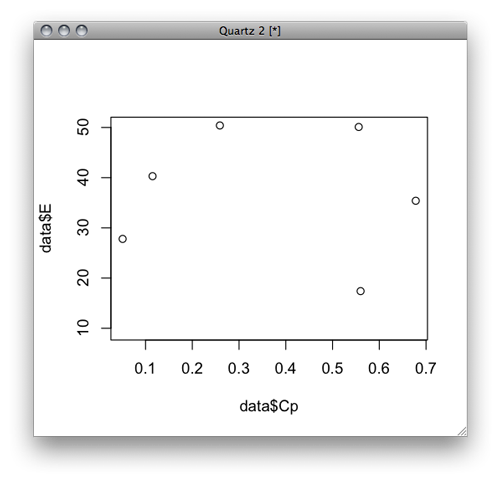
plot(d,peffs)

pk8-4

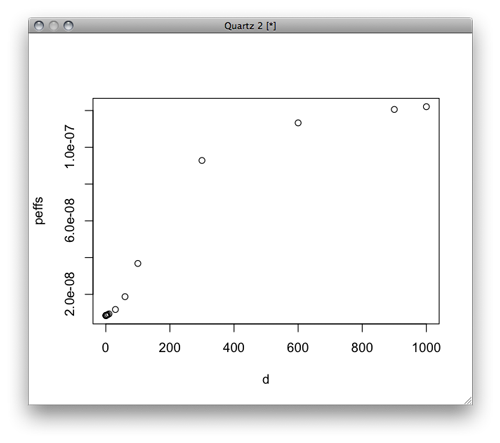
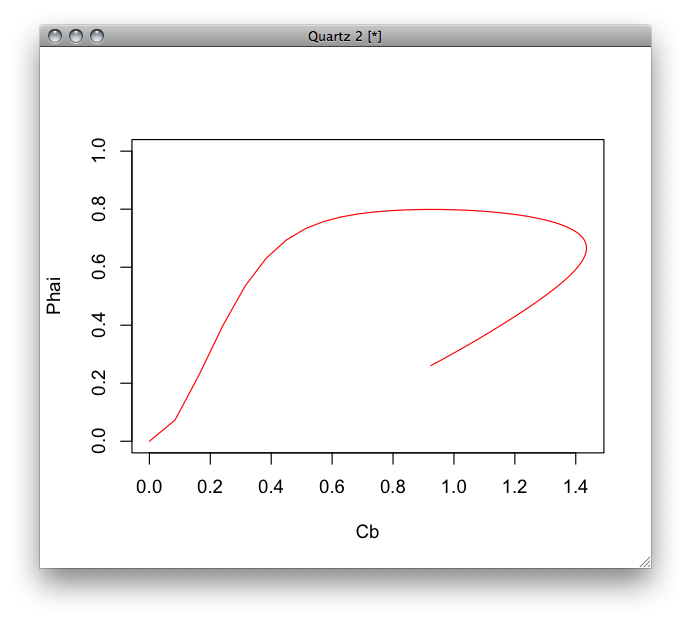
Pgpが飽和した後(高濃度側)ではシグモイド。

設問2

省略

05082009 R DMPK

PK8-3

膜透過性の解釈

ファーマコキネティクス―演習による理解
杉山雄一,山下伸二,加藤基浩
南山堂 / ￥ 6,300 ()
通常2～5週間以内に発送

> Mw = 350
> pKa = 9.5
> sigma = 1.0
> R = 8.62
> e_g = 1.22
> kai = 0.7
> Nav = 6.02 * 10^23
> kb = 1.38 * 10 ^ -16
> T = 273.15 + 37
> n = 0.006915
> r <- (3*Mw/(4*pi*Nav*sigma))^(1/3)
> r
[1] 5.17759e-08
> D <- kb*T/(6*pi*n*r)
> D
[1] 6.342054e-06

> r= 5.17759 # A
> F_r_R <- (1-(r/R))^2*(1-2.104*(r/R)+2.109*(r/R)^3-0.95*(r/R)^5)
> F_r_R
[1] 0.01897611
> r= 5.17759
> F_r_R <- (1-(r/R))^2*(1-2.104*(r/R)+2.109*(r/R)^3-0.95*(r/R)^5)
> F_r_R
[1] 0.0189761
> Ppara <- e_g*D*F_r_R*(kai/(1-exp(-kai)))
> Ppara
[1] 2.041593e-07
> 2.041593e-07/0.42e-6 * 100
[1] 48.60936 # %

05082009 R DMPK

PK8-2

経口投与量とAUCの関係

ファーマコキネティクス―演習による理解
杉山雄一,山下伸二,加藤基浩
南山堂 / ￥ 6,300 ()
通常2～5週間以内に発送

設問1

> data <- read.csv("/Users/kzfm/PK/pk8-2.csv")
> data$dose*1000/(data$AUCp_oral*0.8)
[1]  833.3333 1059.3220 2155.1724

設問2

CLtot(iv)は

> 10*1000/(45*0.8)
[1] 277.7778

題意よりCLh = CLtot(iv) さらにEh*Qh = CLhだから

> Eh <- 277.7778/1500
> Eh
[1] 0.1851852

> Foral <- 277.7778/833.3333
> Foral
[1] 0.3333334

> Fa <- Foral/(1-Eh)
> Fa
[1] 0.409091

設問3

Faで考える

05082009 R DMPK

PK8-1

幾つかの消化管吸収性評価モデル

ファーマコキネティクス―演習による理解
杉山雄一,山下伸二,加藤基浩
南山堂 / ￥ 6,300 ()
通常2～5週間以内に発送

設問1

logM-logM0 = -ka*tより ka = (logM0 - logM)/t = (log(100)-log(20*3.25))/15

> (log(100)-log(20*3.25))/15
[1] 0.02871886

Peff = ka*V/(2*pi*r*L)

ここで r = sqrt(0.1/pi)

> ka*1/(2*pi*0.178*12.5)/60
[1] 3.423782e-05 # cm/sec

設問2

単回灌流試験。水の吸収、分泌補正の項を入れて、定常状態の幾つかの平均を取る。

設問3

plotしてみて直線になっているポイントを選択。

> time <- c(0,15,30,45,60)
> conc <- c(0,0.12,0.28,0.52,0.75)
> plot(time,conc)
> mylist = list(time=time[3:5],conc=conc[3:5])
> data <- data.frame(mylist)
> mylist = list(time=time[3:5],conc=conc[3:5]*2.6)
> data <- data.frame(mylist)
> res<-lm(conc ~ time,data)
> res

Call:
lm(formula = conc ~ time, data = data)

Coefficients:
(Intercept)         time  
   -0.48967      0.04073  

Peff = 0.04073/4.2/100 = 9.69762e-05

設問4

省略

05082009 R DMPK

PK7-2

PK-PD

multirtが必要なのだけど、これをRでどうやるかわからんのでスキップ

ファーマコキネティクス―演習による理解
杉山雄一,山下伸二,加藤基浩
南山堂 / ￥ 6,300 ()
通常2～5週間以内に発送

04082009 R DMPK

PK7-1

PK-PDモデリング

ファーマコキネティクス―演習による理解
杉山雄一,山下伸二,加藤基浩
南山堂 / ￥ 6,300 ()
通常2～5週間以内に発送

設問1

> data <- read.csv("/Users/kzfm/PK/pk7-1.csv")
> data
  time    Cp    E
k  0.0 0.000  0.0
a  0.2 0.309   NA
b  0.5 0.560 17.4
c  1.5 0.678 35.4
d  2.0 0.556 50.1
e  3.0 0.386   NA
f  4.0 0.259 50.4
g  6.0 0.115 40.3
h  8.0 0.051 27.8
i  9.0    NA 22.0
j 12.0    NA  9.3
> plot(data$Cp,data$E)

半時計周りのヒステリシス

pk7-1-1

設問2

pk7-1-2

> nls(Cp ~ alpha*(exp(-beta*time)-exp(-gamma*time)),data[c("time","Cp")],start=list(alpha=100,beta=10,gamma=0.1))
Nonlinear regression model
  model:  Cp ~ alpha * (exp(-beta * time) - exp(-gamma * time)) 
   data:  data[c("time", "Cp")] 
  alpha    beta   gamma 
-1.3322  1.8587  0.4085 
 residual sum-of-squares: 2.501e-07

Number of iterations to convergence: 8 
Achieved convergence tolerance: 8.835e-07 

ka = 1.8587
ke = 0.4085

つまりCp = -1.3322 (exp(-1.8587t)-exp(-0.4085*t))で

Ce = 1.3322*ke0/(ke0-0.4085)*exp(-0.4085*t) - \
1.3322*ke0/(ke0-1.8587)*exp(-1.8587*t) + 1.931666*ke0/((ke0-0.4085)*\
(ke0-1.8587))*exp(-ke0*t)

これをE=Emax*Ce/(EC50+Ce)=100*Ce/(EC50+Ce)に代入してフィッティング

> nls(E ~ 100*(1.3322*ke0/(ke0-0.4085)*exp(-0.4085*time) - \
1.3322*ke0/(ke0-1.8587)*exp(-1.8587*time) + 1.931666*ke0/((ke0-0.4085)* \
(ke0-1.8587))*exp(-ke0*time))/(EC50 + (1.3322*ke0/(ke0-0.4085)*exp(-0.4085*time) \
- 1.3322*ke0/(ke0-1.8587)*exp(-1.8587*time) + 1.931666*ke0/((ke0-0.4085)*\
(ke0-1.8587))*exp(-ke0*time))),data[c("time","E")],start=list(ke0=0.2,EC50=0.1))
Nonlinear regression model
  model:  E ~ 100 * (1.3322 * ke0/(ke0 - 0.4085) * exp(-0.4085 * time) \
 -      1.3322 * ke0/(ke0 - 1.8587) * exp(-1.8587 * time) + 1.931666 * \
 ke0/((ke0 - 0.4085) * (ke0 - 1.8587)) * exp(-ke0 * time))/ \
(EC50 + (1.3322 * ke0/(ke0 - 0.4085) * exp(-0.4085 * time) - 1.3322 *
ke0/(ke0 - 1.8587) * exp(-1.8587 * time) + 1.931666 * ke0/((ke0 - 0.4085) * (ke0 - 1.8587)) * exp(-ke0 * time))) 
   data:  data[c("time", "E")] 
   ke0   EC50 
0.4807 0.3595 
 residual sum-of-squares: 0.01642

Number of iterations to convergence: 6 
Achieved convergence tolerance: 2.781e-07

結果

Ce = 8.869647*exp(-0.4085*t) + 0.4647232*exp(-1.8587*t) -9.332967*exp(-0.4807*t)

E = 100*(8.869647*exp(-0.4085*t) + 0.4647232*exp(-1.8587*t) - \
9.332967*exp(-0.4807*t))/(0.3595 + 8.869647*exp(-0.4085*t) + \
0.4647232*exp(-1.8587*t) - 9.332967*exp(-0.4807*t))

> plot(f,xlim=c(0,12),ylim=c(0,60),xlab="Time(hour)")
> plot(f,xlim=c(0,12),ylim=c(0,60),xlab="Time(hour)",ylab="E")
> par(new=T)
> plot(data$time,data$E,xlim=c(0,12),ylim=c(0,60),xlab="",ylab="",axes=F,type="p",col="blue")

pk7-1-3

設問3

CpとEの計算値も一致していることを確かめる

設問2のCeを求める際のラプラス変換があやふやだったのと、別解として用意されてあった連立微分方程式をRでフィッティングさせる方法が分からなかった。

01082009 R DMPK

PK5-3

ヒト in vivo の予測

ファーマコキネティクス―演習による理解
杉山雄一,山下伸二,加藤基浩
南山堂 / ￥ 6,300 ()
在庫あり。

> data$time
 [1]   1   2   3   5   7   8  10  20  30  60  90 120
> library(PK)
> data <- read.csv("/Users/kzfm/PK/pk53.csv")
> auc.complete(conc=data$conc, time=data$time)
Estimation for a complete data design

                  AUC      AUMC
observed     172.9950  7183.805
interpolated       NA        NA
infinity     220.5125 16772.150

血漿中濃度だから血液中濃度に変換

> RB = 1.2
> AUCb = 220.5125 * 1.2
> AUCb
[1] 264.615

0.265 umol*min/mL

肝での全代謝物をAUCbで除すればよいので

> CLh = (0.921+0.671)/0.265
> CLh
[1] 6.007547

> fp =0.78
> Rb = 1.20
> Fh = 1-CLh/Qh
> Fh
[1] 0.8998742

> F <- function(a){4*a/((1+a)^2*exp((a-1)/2/0.17)-(1-a)^2*exp(-(a+1)/2/0.17))-0.900}
> uniroot(f,c(0.1,10))
$root
[1] 1.035727

$f.root
[1] -2.312838e-05

$iter
[1] 11

$estim.prec
[1] 6.103516e-05

> res <- uniroot(f,c(0.1,10))

> RN <- (res$root^2 - 1)/(4*DN)
> CLh_uint = RN*Qh/fb
> CLh_uint
[1] 9.872855

> data = read.csv("/Users/kzfm/PK/pk53_2.csv")
> data
  time qrat qhuman
a    5  6.5    7.9
b   10 13.8   16.1
c   15 19.9   24.7
d   20 26.6   32.0
e   30 39.3   46.2
f   60 60.8   72.9
g   90 73.2   82.0

> rat_res <- lm(data$qrat[1:5]/0.1 ~ data$time[1:5])
> rat_res

Call:
lm(formula = data$qrat[1:5]/0.1 ~ data$time[1:5])

Coefficients:
   (Intercept)  data$time[1:5]  
         3.595          13.038  

> human_res <- lm(data$qhuman[1:5]/0.1 ~ data$time[1:5])
> human_res

Call:
lm(formula = data$qhuman[1:5]/0.1 ~ data$time[1:5])

Coefficients:
   (Intercept)  data$time[1:5]  
         8.784          15.314  

> CLh_uint_rat = 13.038/0.4*51.2/1000*44
> CLh_uint_human = 15.314/0.5*52.5/1000*24.3
> CLh_uint_rat
[1] 73.43002
> CLh_uint_human
[1] 39.07367

ラットのin vivoのデータとin vitroのデータの比からヒトのin vitroのデータを用いヒトin vivoを予測。本の計算はミクロソーム蛋白の量を間違ってる(問題文は0.1なのに0.5で計算してる)けど、最終的に比になっているので結果に影響はないようだ。

> CLh_uint_human * (9.872855/CLh_uint_rat)
[1] 5.253556

01082009 R DMPK

PK5-2

CYPの分子種毎のデータから肝クリアランスを予測

ファーマコキネティクス―演習による理解
杉山雄一,山下伸二,加藤基浩
南山堂 / ￥ 6,300 ()
在庫あり。

本のCYP2D6の計算間違ってるね。

> CLh_uint_3A4 = 0.0896 /(10 * 0.4)/0.056
> CLh_uint_1A2 = 0.0462 /(10 * 0.42)/0.110
> CLh_uint_2D6 = 0.0036 /(10 * 0.30)/0.04
> CLh_uint_3A4
[1] 0.4
> CLh_uint_1A2
[1] 0.1
> CLh_uint_2D6
[1] 0.03

体重あたりになおして

> CLh_uint = (CLh_uint_3A4 * 5 + CLh_uint_1A2 * 2.2 + CLh_uint_2D6 * 0.26)*24.3
> CLh_uint 
[1] 54.13554

あとはクリアランスとFhを求める

> fp = 0.2
> Rb = 0.4
> fb = fp/Rb
> Qh = 20
> DN = 0.17
> RN = fb*CLh_uint/Qh
> a = sqrt(1+4*RN*DN)
> Fh = 4*a/((1+a)^2*exp((a-1)/2/DN - (1-a)^2*exp(-(a+1)/2/DN)))
> Fh
[1] 0.3131986
> CLh = Qh*(1-Fh)
> CLh
[1] 13.73603

31072009 R DMPK

PK5-1

アニマルスケールアップによるヒトクリアランス予測

ファーマコキネティクス―演習による理解
杉山雄一,山下伸二,加藤基浩
南山堂 / ￥ 6,300 ()
在庫あり。

設問1

164.6/3*52.5*24.3/1000 CLh_uint = 69.99615 mL/min/kg

Fh = (Qh-CLh)/Qh

well-stirredはCLh = Qh*fb*CLh_uint/(Qh + fb*CLh_uint)

> Qh = 20
> fb = 0.08/0.64
> CLh = Qh*fb*CLh_uint/(Qh + fb*CLh_uint)
> CLh
[1] 6.086724
> Fh = (Qh-CLh)/Qh
> Fh
[1] 0.6956638

paralle tubeはCLh = Qh*(1-exp(-fb*CLh_uint/Qh))

> CLh = Qh*(1-exp(-fb*CLh_uint/Qh))
> CLh
[1] 7.086719
> Fh = (Qh-CLh)/Qh
> Fh
[1] 0.645664

dispersionは問題文から

> RN = fb*CLh_uint/Qh
> DN = 0.17
> a = sqrt(1+4*RN*DN)
> Fh = 4*a/((1+a)^2*exp((a-1)/2/DN - (1-a)^2*exp(-(a+1)/2/DN)))
> Fh
[1] 0.6615078
> CLh = Qh*(1-Fh)
> CLh
[1] 6.769845

設問2

ラットのクリアランス

> CLtot = 0.6/20*1000
> CLtot
[1] 30
> CLr = 0.2/20*1000
> CLr
[1] 10
> CLh = CLtot - CLr
> CLh
[1] 20

> GFR = 7.6
> Qr = 40.0
> B = CLr -fb*GFR
> CLr_uint = B*Qr/(Qr-B)/fb
> CLr_uint
[1] 120.1560

アロメトリー

> (92.5 * 60^0.88)/60
[1] 56.59311

> fb = 0.08/0.64
> Qr = 16
> GFR = 1.8
> CLr_uint = (92.5 * 60^0.88)/60
> CLr = fb*GFR + Qr*fb*CLr_uint/(Qr+fb*CLr_uint)
> CLr
[1] 5.130328

設問3

AUCb,iv = Dose/CLtot CLtot = CLh + CLr

ここでCLrは設問2で求めた。 CLhは設問1のを使えばいい。

設問4

AUCb,oral = Fg*Fh*Dose/CLtot 問題よりFg=1 あとは設問3と同様

29072009 R DMPK

PK4-2

脳内のレセプターと薬物の結合のシミュレーション

ファーマコキネティクス―演習による理解
杉山雄一,山下伸二,加藤基浩
南山堂 / ￥ 6,300 ()
在庫あり。

odesolveで血中濃度が時間依存的に減少するとき(時間の関数になっているとき)どういう風に書けばいいのか悩んだが

Cp <- dose/mwt*(50*exp(-0.1*t) + 125*exp(-0.025*t))

とtそのまま使えることがわかったので解決

library(odesolve)
times=c(0,(1:120))
params = c(fb=0.2,mwt=250, Kp=8.0, kon=2,koff=0.2,Rt=1,Vt=1,Q=1,dose=0.2)

dydt <- function(t,y,p){
fb <- p['fb']
Kp <- p['Kp']
kon <- p['kon']
koff <- p['koff']
Rt <- p['Rt']
Vt <- p['Vt']
Q <- p['Q']
dose <- p['dose']
mwt <- p['mwt']

Cp <- dose/mwt*(50*exp(-0.1*t) + 125*exp(-0.025*t))
Ct <- (Q*(Cp-y[1]/Kp)-kon*fb*y[1]/Kp*Rt*(1-y[2])+koff*Rt*y[2])/Vt
PHAI <- kon*fb*y[1]/Kp*(1-y[2])-koff*y[2]
return(list(c(Ct,PHAI)))
}

y <- lsoda(c(Ct=0.0,PHAI=0.0),times,dydt,params)

y02 <- y
params = c(fb=0.2,mwt=250, Kp=8.0, kon=2,koff=0.2,Rt=1,Vt=1,Q=1,dose=1)
y <- lsoda(c(Ct=0.0,PHAI=0.0),times,dydt,params)
y1 <- y
params = c(fb=0.2,mwt=250, Kp=8.0, kon=2,koff=0.2,Rt=1,Vt=1,Q=1,dose=5)
y <- lsoda(c(Ct=0.0,PHAI=0.0),times,dydt,params)
y5 <- y

plot(y02[,1],y02[,3],ylim=c(0,1.0),xlab="time(min)",ylab="Phai",type="l",col="red")
par(new=T)
plot(y1[,1],y1[,3],ylim=c(0,1.0),xlab="",ylab="",axes=F,type="l",col="blue")
par(new=T)
plot(y5[,1],y5[,3],ylim=c(0,1.0),xlab="",ylab="",axes=F,type="l",col="green")

pk4-2-1

plot(y2[,2],y5[,3],ylim=c(0,1.0),xlab="Cb",ylab="Phai",type="l",col="red")

pk4-2-2

ヒステリシスがみられる

もう5年目(wishlistありマス♡)
最近はPythonとDeepLearning
日本酒自粛中
ドラムンベースからミニマルまで
ポケモンGOゆるめ