経口投与量とAUCの関係
ファーマコキネティクス―演習による理解> data <- read.csv("/Users/kzfm/PK/pk8-2.csv")
> data$dose*1000/(data$AUCp_oral*0.8)
[1] 833.3333 1059.3220 2155.1724
CLtot(iv)は
> 10*1000/(45*0.8)
[1] 277.7778
題意よりCLh = CLtot(iv) さらにEh*Qh = CLhだから
> Eh <- 277.7778/1500
> Eh
[1] 0.1851852
> Foral <- 277.7778/833.3333
> Foral
[1] 0.3333334
> Fa <- Foral/(1-Eh)
> Fa
[1] 0.409091
Faで考える
幾つかの消化管吸収性評価モデル
logM-logM0 = -ka*tより ka = (logM0 - logM)/t = (log(100)-log(20*3.25))/15
> (log(100)-log(20*3.25))/15
[1] 0.02871886
Peff = ka*V/(2*pi*r*L)
ここで r = sqrt(0.1/pi)
> ka*1/(2*pi*0.178*12.5)/60
[1] 3.423782e-05 # cm/sec
単回灌流試験。水の吸収、分泌補正の項を 入れて、定常状態の幾つかの平均を取る。
plotしてみて直線になっているポイントを選択。
> time <- c(0,15,30,45,60)
> conc <- c(0,0.12,0.28,0.52,0.75)
> plot(time,conc)
> mylist = list(time=time[3:5],conc=conc[3:5])
> data <- data.frame(mylist)
> mylist = list(time=time[3:5],conc=conc[3:5]*2.6)
> data <- data.frame(mylist)
> res<-lm(conc ~ time,data)
> res
Call:
lm(formula = conc ~ time, data = data)
Coefficients:
(Intercept) time
-0.48967 0.04073
Peff = 0.04073/4.2/100 = 9.69762e-05
省略
草むしりメインで。
それにしてもうちの畑は、土地の利用効率も時間の利用の効率も悪くて、収穫のタイミングがまちまちで、継続的な収穫が出来なかったり、畝の間隔が空きすぎてて雑草が生えやすくなってたりと、ダメなとこだらけだ。隣の畑から色々学ぶことが多いなぁ。
秋撒きはレイアウトとかちゃんと考えてまく。
わけぎと唯一定期的に収穫できるゴーヤ
アシタバとモロヘイヤ。アシタバはどのタイミングで摘み取ればいいのか分からないのでとりあえず放っておいたらでかくなってきた。
04082009 life
先週末から夏の短期休暇で、南伊豆のあたりに、家族4人with犬一匹。犬連れだとコテージとかそんなんしかない感じで宿泊施設の選択肢は狭まるが、（色々と）気にしなければそれなりに楽しい。
子浦海岸で海水浴。海の家すらないこじんまりした海水浴場だが、子供が小さいのでかえって楽。カヌーの教室のゴールにもなってるっぽい。楽しそう、カヌー。今度やる。
で、近場の定食屋さんの今津屋。
あじのてこね寿司と磯炊きご飯。ここは美味しいですな。
泳いで、コテージに戻って、BBQしたり花火したりして就寝。ホピアというところを利用したんだけど、現地で調達できる食材(酒も含めて)はなにもないのと、BBQセットは別料金なので、コンロを持っていれば持参するという手もあった。宿泊者が少なかったというのもあるんだけど風呂はのんびりできてよかった(コテージのユニットは入る気おきんかった)。
二日目は下田〜河津を通って帰るコース。途中下田で昼食。
亀遊で金目のかき揚げ丼と金目の釜飯。
味付けも濃すぎず薄すぎず好み。
帰りに撮った下田。下田の海は芋荒い場みたいだったな。
南伊豆-西伊豆はのんびりできてよいですな。また行きたい。
かいとく丸ねらってるんだけどなぁ。
PK-PDモデリング
> data <- read.csv("/Users/kzfm/PK/pk7-1.csv")
> data
time Cp E
k 0.0 0.000 0.0
a 0.2 0.309 NA
b 0.5 0.560 17.4
c 1.5 0.678 35.4
d 2.0 0.556 50.1
e 3.0 0.386 NA
f 4.0 0.259 50.4
g 6.0 0.115 40.3
h 8.0 0.051 27.8
i 9.0 NA 22.0
j 12.0 NA 9.3
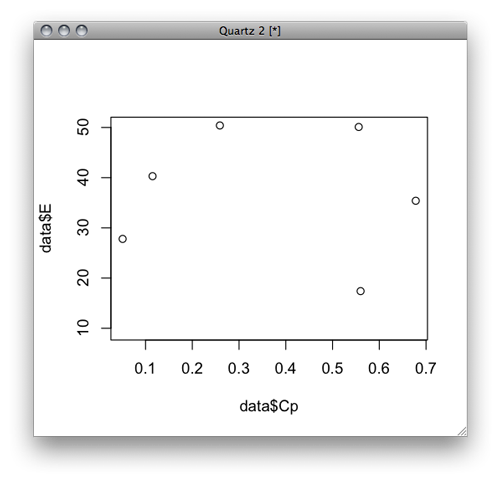
> plot(data$Cp,data$E)
半時計周りのヒステリシス
> nls(Cp ~ alpha*(exp(-beta*time)-exp(-gamma*time)),data[c("time","Cp")],start=list(alpha=100,beta=10,gamma=0.1))
Nonlinear regression model
model: Cp ~ alpha * (exp(-beta * time) - exp(-gamma * time))
data: data[c("time", "Cp")]
alpha beta gamma
-1.3322 1.8587 0.4085
residual sum-of-squares: 2.501e-07
Number of iterations to convergence: 8
Achieved convergence tolerance: 8.835e-07
ka = 1.8587
ke = 0.4085
つまりCp = -1.3322 (exp(-1.8587t)-exp(-0.4085*t))で
Ce = 1.3322*ke0/(ke0-0.4085)*exp(-0.4085*t) - \
1.3322*ke0/(ke0-1.8587)*exp(-1.8587*t) + 1.931666*ke0/((ke0-0.4085)*\
(ke0-1.8587))*exp(-ke0*t)
これをE=Emax*Ce/(EC50+Ce)=100*Ce/(EC50+Ce)に代入してフィッティング
> nls(E ~ 100*(1.3322*ke0/(ke0-0.4085)*exp(-0.4085*time) - \
1.3322*ke0/(ke0-1.8587)*exp(-1.8587*time) + 1.931666*ke0/((ke0-0.4085)* \
(ke0-1.8587))*exp(-ke0*time))/(EC50 + (1.3322*ke0/(ke0-0.4085)*exp(-0.4085*time) \
- 1.3322*ke0/(ke0-1.8587)*exp(-1.8587*time) + 1.931666*ke0/((ke0-0.4085)*\
(ke0-1.8587))*exp(-ke0*time))),data[c("time","E")],start=list(ke0=0.2,EC50=0.1))
Nonlinear regression model
model: E ~ 100 * (1.3322 * ke0/(ke0 - 0.4085) * exp(-0.4085 * time) \
- 1.3322 * ke0/(ke0 - 1.8587) * exp(-1.8587 * time) + 1.931666 * \
ke0/((ke0 - 0.4085) * (ke0 - 1.8587)) * exp(-ke0 * time))/ \
(EC50 + (1.3322 * ke0/(ke0 - 0.4085) * exp(-0.4085 * time) - 1.3322 *
ke0/(ke0 - 1.8587) * exp(-1.8587 * time) + 1.931666 * ke0/((ke0 - 0.4085) * (ke0 - 1.8587)) * exp(-ke0 * time)))
data: data[c("time", "E")]
ke0 EC50
0.4807 0.3595
residual sum-of-squares: 0.01642
Number of iterations to convergence: 6
Achieved convergence tolerance: 2.781e-07
結果
Ce = 8.869647*exp(-0.4085*t) + 0.4647232*exp(-1.8587*t) -9.332967*exp(-0.4807*t)
E = 100*(8.869647*exp(-0.4085*t) + 0.4647232*exp(-1.8587*t) - \
9.332967*exp(-0.4807*t))/(0.3595 + 8.869647*exp(-0.4085*t) + \
0.4647232*exp(-1.8587*t) - 9.332967*exp(-0.4807*t))
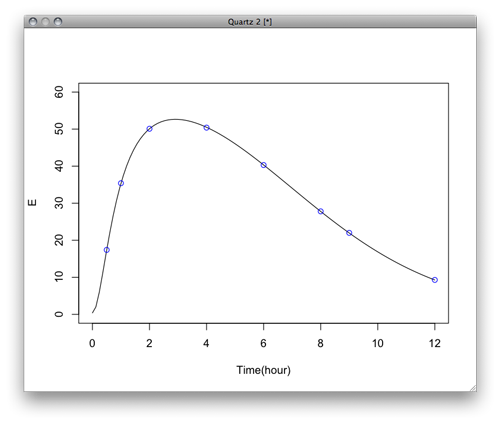
> plot(f,xlim=c(0,12),ylim=c(0,60),xlab="Time(hour)")
> plot(f,xlim=c(0,12),ylim=c(0,60),xlab="Time(hour)",ylab="E")
> par(new=T)
> plot(data$time,data$E,xlim=c(0,12),ylim=c(0,60),xlab="",ylab="",axes=F,type="p",col="blue")
CpとEの計算値も一致していることを確かめる
設問2のCeを求める際のラプラス変換があやふやだったのと、別解として用意されてあった連立微分方程式をRでフィッティングさせる方法が分からなかった。
ヒト in vivo の予測
> data$time
[1] 1 2 3 5 7 8 10 20 30 60 90 120
> library(PK)
> data <- read.csv("/Users/kzfm/PK/pk53.csv")
> auc.complete(conc=data$conc, time=data$time)
Estimation for a complete data design
AUC AUMC
observed 172.9950 7183.805
interpolated NA NA
infinity 220.5125 16772.150
血漿中濃度だから血液中濃度に変換
> RB = 1.2
> AUCb = 220.5125 * 1.2
> AUCb
[1] 264.615
0.265 umol*min/mL
肝での全代謝物をAUCbで除すればよいので
> CLh = (0.921+0.671)/0.265
> CLh
[1] 6.007547
> fp =0.78
> Rb = 1.20
> Fh = 1-CLh/Qh
> Fh
[1] 0.8998742
> F <- function(a){4*a/((1+a)^2*exp((a-1)/2/0.17)-(1-a)^2*exp(-(a+1)/2/0.17))-0.900}
> uniroot(f,c(0.1,10))
$root
[1] 1.035727
$f.root
[1] -2.312838e-05
$iter
[1] 11
$estim.prec
[1] 6.103516e-05
> res <- uniroot(f,c(0.1,10))
> RN <- (res$root^2 - 1)/(4*DN)
> CLh_uint = RN*Qh/fb
> CLh_uint
[1] 9.872855
> data = read.csv("/Users/kzfm/PK/pk53_2.csv")
> data
time qrat qhuman
a 5 6.5 7.9
b 10 13.8 16.1
c 15 19.9 24.7
d 20 26.6 32.0
e 30 39.3 46.2
f 60 60.8 72.9
g 90 73.2 82.0
> rat_res <- lm(data$qrat[1:5]/0.1 ~ data$time[1:5])
> rat_res
Call:
lm(formula = data$qrat[1:5]/0.1 ~ data$time[1:5])
Coefficients:
(Intercept) data$time[1:5]
3.595 13.038
> human_res <- lm(data$qhuman[1:5]/0.1 ~ data$time[1:5])
> human_res
Call:
lm(formula = data$qhuman[1:5]/0.1 ~ data$time[1:5])
Coefficients:
(Intercept) data$time[1:5]
8.784 15.314
> CLh_uint_rat = 13.038/0.4*51.2/1000*44
> CLh_uint_human = 15.314/0.5*52.5/1000*24.3
> CLh_uint_rat
[1] 73.43002
> CLh_uint_human
[1] 39.07367
ラットのin vivoのデータとin vitroのデータの比からヒトのin vitroのデータを用いヒトin vivoを予測。本の計算はミクロソーム蛋白の量を間違ってる(問題文は0.1なのに0.5で計算してる)けど、最終的に比になっているので結果に影響はないようだ。
> CLh_uint_human * (9.872855/CLh_uint_rat)
[1] 5.253556
先週のはなしだけど。あとゴーヤとトマト（雨のせいで収穫時期が遅れて裂けてしまった）も収穫。枝豆は思ったよりは実らなかったな。
そういえば枝豆を抜くときに根にへんな粒がついてて病気か？と思ったんだけど根粒菌だそうだ。しかもレグヘモグロビンのせいで切ると血のような色をしているらしい。
昔研究室で、再構成ミオグロビン作ってたので、これは見とくべきだったと後悔。来年も枝豆植えてやる。
CYPの分子種毎のデータから肝クリアランスを予測
本のCYP2D6の計算間違ってるね。
身近な野菜のなるほど観察記> CLh_uint_3A4 = 0.0896 /(10 * 0.4)/0.056
> CLh_uint_1A2 = 0.0462 /(10 * 0.42)/0.110
> CLh_uint_2D6 = 0.0036 /(10 * 0.30)/0.04
> CLh_uint_3A4
[1] 0.4
> CLh_uint_1A2
[1] 0.1
> CLh_uint_2D6
[1] 0.03
体重あたりになおして
> CLh_uint = (CLh_uint_3A4 * 5 + CLh_uint_1A2 * 2.2 + CLh_uint_2D6 * 0.26)*24.3
> CLh_uint
[1] 54.13554
あとはクリアランスとFhを求める
> fp = 0.2
> Rb = 0.4
> fb = fp/Rb
> Qh = 20
> DN = 0.17
> RN = fb*CLh_uint/Qh
> a = sqrt(1+4*RN*DN)
> Fh = 4*a/((1+a)^2*exp((a-1)/2/DN - (1-a)^2*exp(-(a+1)/2/DN)))
> Fh
[1] 0.3131986
> CLh = Qh*(1-Fh)
> CLh
[1] 13.73603
アニマルスケールアップによるヒトクリアランス予測
164.6/3*52.5*24.3/1000 CLh_uint = 69.99615 mL/min/kg
Fh = (Qh-CLh)/Qh
well-stirredはCLh = Qh*fb*CLh_uint/(Qh + fb*CLh_uint)
> Qh = 20
> fb = 0.08/0.64
> CLh = Qh*fb*CLh_uint/(Qh + fb*CLh_uint)
> CLh
[1] 6.086724
> Fh = (Qh-CLh)/Qh
> Fh
[1] 0.6956638
paralle tubeはCLh = Qh*(1-exp(-fb*CLh_uint/Qh))
> CLh = Qh*(1-exp(-fb*CLh_uint/Qh))
> CLh
[1] 7.086719
> Fh = (Qh-CLh)/Qh
> Fh
[1] 0.645664
dispersionは問題文から
> RN = fb*CLh_uint/Qh
> DN = 0.17
> a = sqrt(1+4*RN*DN)
> Fh = 4*a/((1+a)^2*exp((a-1)/2/DN - (1-a)^2*exp(-(a+1)/2/DN)))
> Fh
[1] 0.6615078
> CLh = Qh*(1-Fh)
> CLh
[1] 6.769845
ラットのクリアランス
> CLtot = 0.6/20*1000
> CLtot
[1] 30
> CLr = 0.2/20*1000
> CLr
[1] 10
> CLh = CLtot - CLr
> CLh
[1] 20
> GFR = 7.6
> Qr = 40.0
> B = CLr -fb*GFR
> CLr_uint = B*Qr/(Qr-B)/fb
> CLr_uint
[1] 120.1560
アロメトリー
> (92.5 * 60^0.88)/60
[1] 56.59311
> fb = 0.08/0.64
> Qr = 16
> GFR = 1.8
> CLr_uint = (92.5 * 60^0.88)/60
> CLr = fb*GFR + Qr*fb*CLr_uint/(Qr+fb*CLr_uint)
> CLr
[1] 5.130328
AUCb,iv = Dose/CLtot CLtot = CLh + CLr
ここでCLrは設問2で求めた。 CLhは設問1のを使えばいい。
AUCb,oral = Fg*Fh*Dose/CLtot 問題よりFg=1 あとは設問3と同様