04042010 Python machinelearning
MCMCとグラフィカルモデリング
 Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)
Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)Stephen Marsland
Chapman & Hall / ¥ 6,700 ()
在庫あり。
この本だけではちょっと理解不足なので、PRMLとかまた読み返そう。
04042010 Python machinelearning
MCMCとグラフィカルモデリング
 Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)
Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)この本だけではちょっと理解不足なので、PRMLとかまた読み返そう。
20032010 Python machinelearning
強化学習
 Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)
Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)いくつかの問題点も指摘されている。例えば Q学習による理論的保証は値の収束性のみであり収束途中の値には具体的な合理性が認められないため学習途中の結果を近似解として用いにくい、パラメータの変化に敏感でありその調整に多くの手間が必要であるなどがある。
18032010 Python matplotlib machinelearning
遺伝アルゴリズム
 Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)
Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)Four Peaks Problemってのがあるらしい。目的関数が
目的関数はこんな感じ。
#!/usr/bin/env python
# -*- encoding:utf-8 -*-
from itertools import takewhile
def o(bits):
return len(list(takewhile(lambda x: x == 1,bits)))
def z(bits):
return len(list(takewhile(lambda x: x == 0,reversed(bits))))
def f(bits):
reward = 100 if o(bits) > 10 and z(bits) > 10 else 0
return max(o(bits),z(bits)) + reward
if __name__ == "__main__":
bits1 = [1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
bits2 = [1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
for bits in [bits1,bits2]:
print "score: %d %s" % (f(bits),bits)
#score: 20 [1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
#score: 114 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
要するに素直に探索していくとローカルミニマムに落ちるようになっていて、ピークの数が4つあるのでFour Peaks Problem
連続した1,0の長さでcontour plotを描いた。
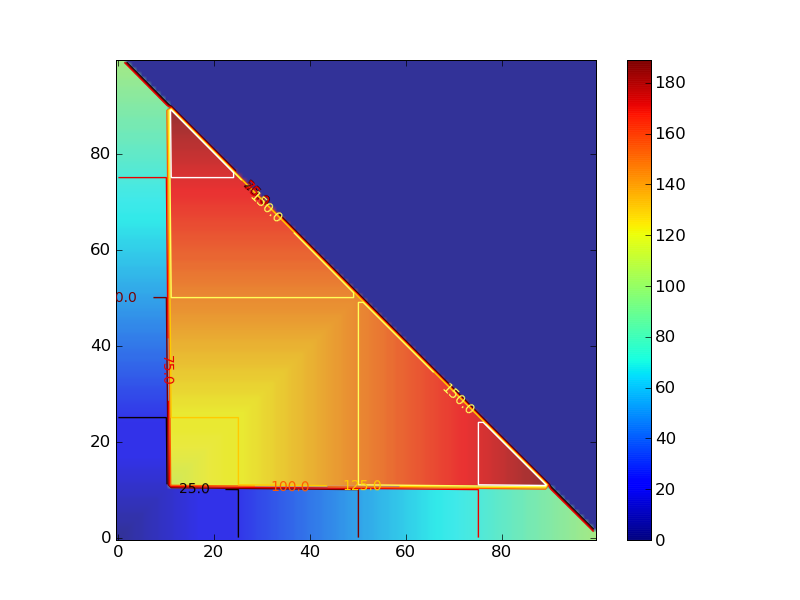
#!/usr/bin/env python
# -*- encoding:utf-8 -*-
def sim_score():
for x in range(100):
for y in range(100):
if x + y > 100:
yield 0
else:
score = four_peak(x,y)
yield score
def four_peak(x,y):
reward = 100 if (x > 10 and y > 10) else 0
score = max(x,y) + reward
return score
if __name__ == "__main__":
from pylab import *
delta = 1
x = arange(0, 100, delta)
y = arange(0, 100, delta)
X, Y = meshgrid(x, y)
Z = array([z for z in sim_score()])
Z.shape = 100,100
im = imshow(Z,origin='lower' ,alpha=.9)
colorbar(im)
cset = contour(X,Y,Z)
clabel(cset,inline=1,fmt='%1.1f',fontsize=10)
hot()
savefig('4peaks.png')
14032010 Python machinelearning
Optimization and Search
 Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)
Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)共役勾配法とか。
章としてはあんまそそられなかった。
14032010 Python machinelearning
次元縮約のアルゴリズム。LDA,PCA,Kernel PCA,ICA,LLE,Isomapあたり。
 Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)
Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)後半部分がちゃんと理解出来ていない。10.2.1でPCAと多層パーセプトロンの関連性を論じているのだけど、そこがよくわからなかった。あとLLE,MDS,Isomapをきちんと理解してないので、ちゃんと読んで一回実装してみる必要がある。
09032010 Python machinelearning
Unsupervised Learning。なかなか面白かった。
 Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)
Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)K-meansの話から入って、K-Meansは一層のニューラルネットで表現することが出来ることを示していく。ニューラルネットで表現されたK-Meansはオンライン更新できるので、入力を一度に読み込まなくて良い(はず)。
そのあとSOMだったけど、SOMは知ってるので流した。
07032010 Python machinelearning
EM Algorithmとkd-Tree
 Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)
Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)内容はPRMLのほうが詳しい。Machine Leaningのほうはコードを読んで実装を理解するって感じだな。
kd-Treeは使ったことなかったけど、近傍探索はよく使うので、覚えておいて自由に使えるようにしようかな。
01112009 Python machinelearning
Machine Learning 4章
 Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)
Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)scipyにはB-splinesが用意されているのでそれを使ってみる
from pylab import *
from numpy import *
from scipy.signal import cspline1d, cspline1d_eval
x = arange(-3,10,0.05)
y = 2.5 * exp(-(x)**2/9) + 3.2 * exp(-(x-0.5)**2/4) + random.normal(0.0, 1.0, len(x))
spline = cspline1d(y,100)
xbar = arange(-5,15,0.1)
ybar = cspline1d_eval(spline, xbar, dx=x[1]-x[0], x0=x[0])
plot(x,y,'.')
plot(xbar,ybar)
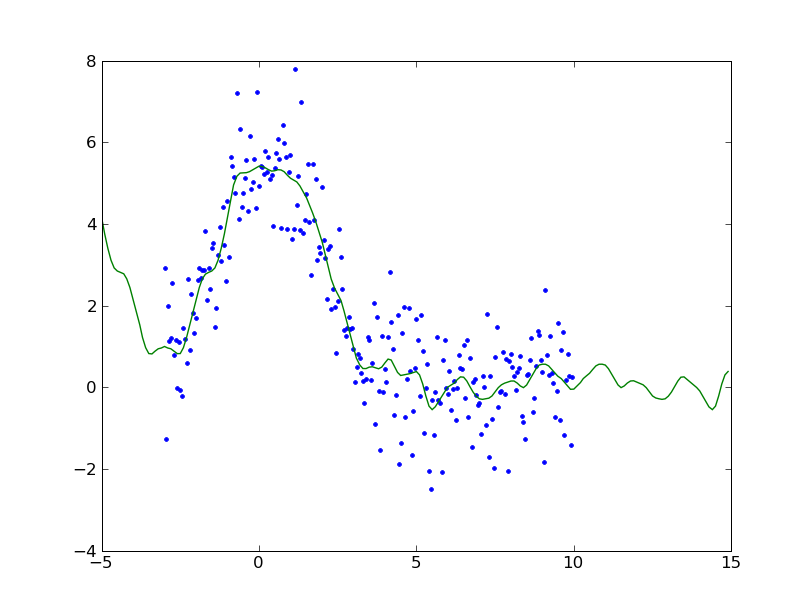
28102009 Python machinelearning
Machine Learning 3章
 Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)
Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)要するにbackwars phaseを実装すればいいんでしょ?的な。実際書いてみると逆に誤差を伝播している感がある。
# Code from Chapter 3 of Machine Learning: An Algorithmic Perspective
# by Stephen Marsland (http://seat.massey.ac.nz/personal/s.r.marsland/MLBook.html)
# You are free to use, change, or redistribute the code in any way you wish for
# non-commercial purposes, but please maintain the name of the original author.
# This code comes with no warranty of any kind.
# Stephen Marsland, 2008
# modifiled by kzfm 2009
from numpy import *
inputs = array([[0,0],[0,1],[1,0],[1,1]])
targets = array([[0],[1],[1],[0]])
ndata,nin = shape(inputs)
nout = shape(targets)[1]
nhidden = 2
beta = 1
momentum = 0.9
eta = 0.25
niterations = 10001
weights1 = (random.rand(nin+1,nhidden)-0.5) * 2/sqrt(nin)
weights2 = (random.rand(nhidden+1,nout)-0.5) * 2/sqrt(nhidden)
# train
inputs = concatenate((inputs,-ones((ndata,1))),axis=1)
change = range(ndata)
updatew1 = zeros((shape(weights1)))
updatew2 = zeros((shape(weights2)))
for n in range(niterations):
hidden = concatenate((1.0/(1.0+exp(-beta * dot(inputs,weights1))), -ones((shape(inputs)[0],1))),axis=1)
outputs = 1.0 / (1.0+exp(-beta * dot(hidden,weights2)))
error = 0.5 * sum((targets-outputs)**2)
if (mod(n,1000)==0): print "Iteration: ",n, " Error: ",error
deltao = (targets-outputs) * outputs * (1.0-outputs)
deltah = hidden * (1.0-hidden) * (dot(deltao,transpose(weights2)))
updatew1 = eta*(dot(transpose(inputs),deltah[:,:-1])) + momentum*updatew1
updatew2 = eta*(dot(transpose(hidden),deltao)) + momentum*updatew2
weights1 += updatew1
weights2 += updatew2
random.shuffle(change)
inputs = inputs[change,:]
targets = targets[change,:]
ちなみに、創薬系でのニューラルネットは論文とかは多いけど、実務ではあんまり使われないと思う(特にケミストよりになればなるほど)。というのは、実務においてはゴールするためにはこういうロジックで合成すればよろしいみたいな指針を提示しないといけないが、ニューラルネットでつくったモデルだとそういう解釈がしづらい。
なんか物がたくさんあって、フィルタリングしたいという要求には答えられるけど、何をどういう指針に従って創るかみたいな、創造(製造)律速な問題には使いにくい。
じゃぁ神経系は創造的ではないのかというと、それはまた違うんじゃないかなぁと思ったりもする。モデル化があれなのかなぁとも思うのだけど、、、、
26102009 Python machinelearning
Machine Learningを読んでいる
 Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)
Machine Learning: An Algorithmic Perspective (Chapman & Hall/Crc Machine Learning & Patrtern Recognition)numpyでパーセプトロンでORを訓練してみた(なにげにパーセプトロンとかニューラルネットワークの実装は初めてだったりする)。
from numpy import *
inputs = array([[0,0],[0,1],[1,0],[1,1]])
targets = array([[0],[1],[1],[1]])
nIterations = 6
eta = 0.25
nData = shape(inputs)[0]
nIn = shape(inputs)[1]
nOut = shape(targets)[1]
weights = random.rand(nIn+1,nOut)
inputs = concatenate((inputs,-ones((nData,1))),axis=1)
for i in range(nIterations):
outputs = where(dot(inputs,weights)>0,1,0)
weights += eta*dot(transpose(inputs),targets-outputs)
print "Iter: %d" % i
print weights
print "Final outputs are:"
print where(dot(inputs,weights)>0,1,0)
この本は、アルゴリズムに関して説明するのがメインの本らしいので、コードの解説はあんまなくて、詳しくはサンプルコード読めということらしいが、もう少し読んでみないとわからん。