マルコフ連鎖モンテカルロ法の5-2をJAGSで
モデル
model
{
for( i in 1 : Num ) {
rc[i] ~ dbin(pc[i], nc[i]);
rt[i] ~ dbin(pt[i], nt[i]);
logit(pc[i]) <- mu[i];
logit(pt[i]) <- mu[i] + delta[i];
mu[i] ~ dnorm(0.0,1.0E-5);
delta[i] ~ dnorm(d, tau);
}
d ~ dnorm(0.0,1.0E-6);
tau ~ dgamma(0.001,0.001);
delta.new ~ dnorm(d, tau);
sigma <- 1 / sqrt(tau);
}
Rのコード
library(rjags)
data <- list(rt = c(49, 44, 102, 32, 85, 246, 1570),
nt = c(615, 758, 832, 317, 810, 2267, 8587),
rc = c(67, 64, 126, 38, 52, 219, 1720),
nc = c(624, 771, 850, 309, 406, 2257, 8600),
Num = 7)
inits <- list(d = 0, delta.new = 0, tau=1,
mu = c(0, 0, 0, 0, 0, 0, 0),
delta = c(0, 0, 0, 0, 0, 0, 0))
m <- jags.model(
file = "model.txt",
data = data,
inits = list(inits),
n.chains = 1
)
update(m,5000)
x <- coda.samples(
m,
c("d","sigma"),
thin = 1, n.iter = 15000
)
summary(x)
plot(x)
結果
> summary(x)
Iterations = 6001:21000
Thinning interval = 1
Number of chains = 1
Sample size per chain = 15000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
d -0.1400 0.08028 0.0006555 0.001885
sigma 0.1285 0.08188 0.0006686 0.002196
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
d -0.31570 -0.18244 -0.1338 -0.0908 0.003366
sigma 0.02855 0.06916 0.1110 0.1672 0.331475
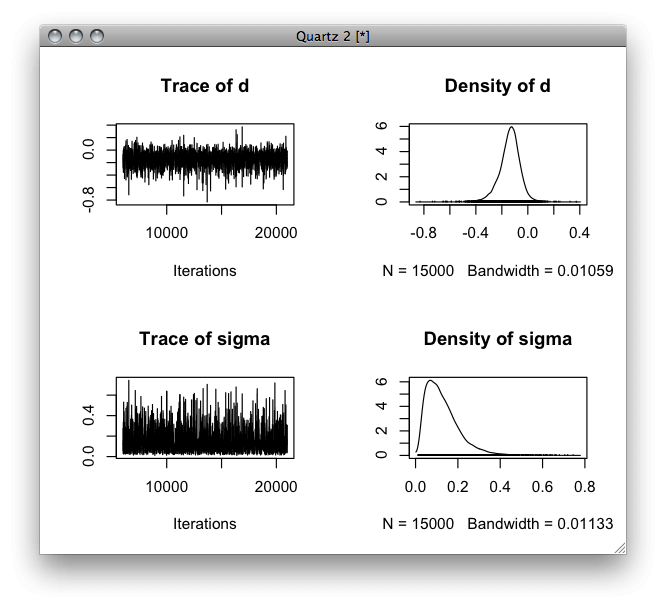

 マルコフ連鎖モンテカルロ法 (統計ライブラリー)
マルコフ連鎖モンテカルロ法 (統計ライブラリー)