エッジをネガティブな力とした時に、エッジを構成しないノードの最大集合を求める問題を最大安定集合問題といい、これは補グラフの最大クリーク問題と同値である。

メタヒューリスティクスの数理
久保 幹雄,J. P. ペドロソ
共立出版 / ￥ 3,675 ()
在庫あり。

networkx用のコード

if __name__ == "__main__":
    import networkx as nx
    import matplotlib.pyplot as plt

    num_nodes = 100
    nodes,edges = rnd_graph(num_nodes,0.5)
    cedges = complement(nodes,edges)
    adj = adjacent(nodes, cedges)
    max_iterations = 1000
    tabulength = len(nodes)/10

    G=nx.Graph()
    for i in range(num_nodes):
        G.add_node(i)
    for i in range(num_nodes-1):
        for j in adj[i]:
            if i < j:
                G.add_edge(i,j)

    pos=nx.spring_layout(G)
    sol = construct(nodes,adj)
    xcard, xinfeas, xb = evaluate(nodes, adj, sol)
    sol, card = tabu_search(nodes, adj, sol, max_iterations, tabulength)

    rnodelist = []
    bnodelist = []
    for i in range(num_nodes):
        if i in sol:
            rnodelist.append(i)
        else:
            bnodelist.append(i)

    redges = []
    for i in range(len(rnodelist)-1):
        for j in range(i+1,len(rnodelist)):
                redges.append((rnodelist[i],rnodelist[j]))


    nx.draw(G,pos,nodelist=rnodelist,edgelist=redges,node_color='r')
    nx.draw(G,pos,nodelist=bnodelist,edgelist=[],node_color='b')
    plt.savefig("max_clique.png")

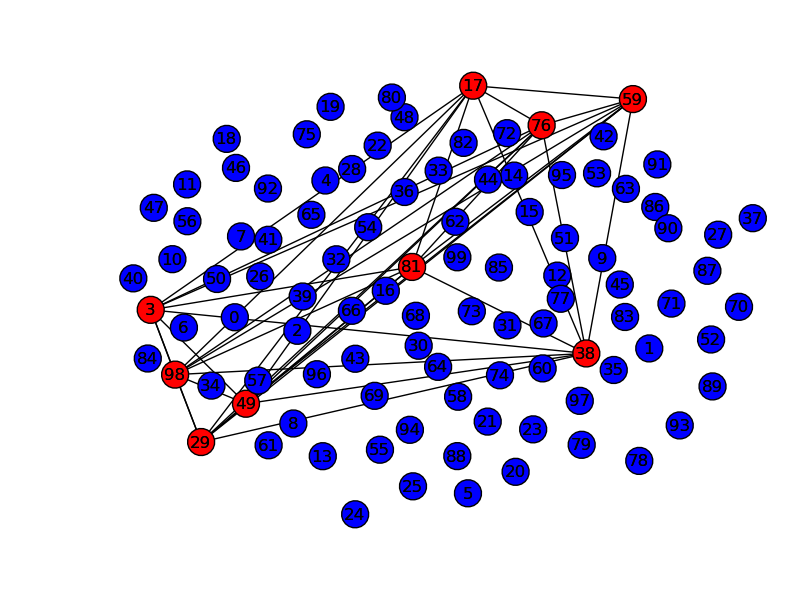
例えばHTSヒットの化合物群をMCSベースでネットワークをつくり、最大安定集合問題として解けば、部分構造ベースで非類似度の高い化合物セットを抽出できる（はず）。まぁこういうのはむしろパテントを対象とするべきなのかも。

問題はエッジをどう定義するかなんだけどなぁ(MCSで完璧とも思えないし)。いい方法ないもんかな。