odesolveを覚えるためにロトカ=ヴォルテラの方程式サンプルを。
lvmodel <- function(t, x, parms) {
s <- x[1] # substrate
p <- x[2] # producer
k <- x[3] # consumer
with(as.list(parms),{
import <- approx(signal$times, signal$import, t)$y
ds <- import - b*s*p + g*k
dp <- c*s*p - d*k*p
dk <- e*p*k - f*k
res<-c(ds, dp, dk)
list(res)
})
}
## vector of timesteps
times <- seq(0, 100, length=101)
## external signal with rectangle impulse
signal <- as.data.frame(list(times = times,
import = rep(0,length(times))))
signal$import[signal$times >= 10 & signal$times <=11] <- 0.2
## Parameters for steady state conditions
parms <- c(a=0.0, b=0.0, c=0.1, d=0.1, e=0.1, f=0.1, g=0.0)
## Start values for steady state
y<-xstart <- c(s=1, p=1, k=1)
## Classical RK4 with fixed time step
out1 <- as.data.frame(rk4(xstart, times, lvmodel, parms))
## LSODA (default step size)
out2 <- as.data.frame(lsoda(xstart, times, lvmodel, parms))
## LSODA: with fixed maximum time step
out3 <- as.data.frame(lsoda(xstart, times, lvmodel, parms, hmax=1))
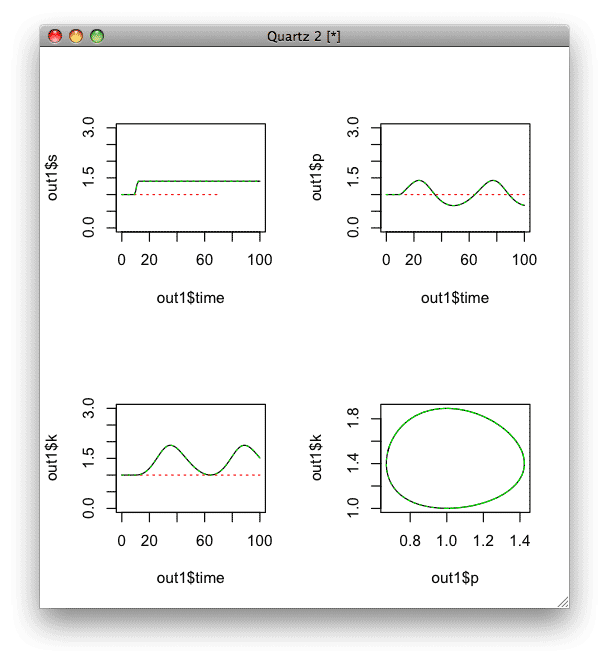
par(mfrow=c(2,2))
plot (out1$time, out1$s, type="l", ylim=c(0,3))
lines(out2$time, out2$s, col="red", lty="dotted")
lines(out3$time, out3$s, col="green", lty="dotted")
plot (out1$time, out1$p, type="l", ylim=c(0,3))
lines(out2$time, out2$p, col="red", lty="dotted")
lines(out3$time, out3$p, col="green", lty="dotted")
plot (out1$time, out1$k, type="l", ylim=c(0,3))
lines(out2$time, out2$k, col="red", lty="dotted")
lines(out3$time, out3$k, col="green", lty="dotted")
plot (out1$p, out1$k, type="l")
lines(out2$p, out2$k, col="red", lty="dotted")
lines(out3$p, out3$k, col="green", lty="dotted")
参考
